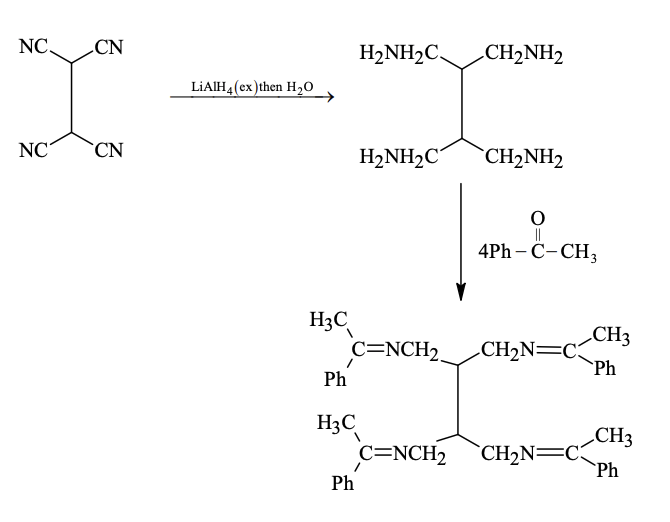
Solution
Analysis of the given sets:
Domain \( S = (0, 1) \cup (1, 2) \cup (3, 4) \). This set is a union of three disjoint open intervals. It contains infinitely many elements (cardinality of the continuum).
Codomain \( T = \{0, 1, 2, 3\} \). This set is finite with 4 elements.
Evaluating Statement (A):
The number of functions from a set \( S \) to a set \( T \) is given by \( |T|^{|S|} \). Here, \( |S| = \infty \) and \( |T| = 4 \).
Total functions = \( 4^{\infty} \), which is infinite.
Statement (A) is True.
Evaluating Statement (B):
A strictly increasing function \( f: S \to T \) requires that for any distinct \( x_1, x_2 \in S \) with \( x_1
< x_2 \), \( f(x_1) < f(x_2) \). This implies \( f \) must be injective (one-to-one).
By the Pigeonhole Principle, it is impossible to map an infinite set injectively into a finite set of 4 elements. Therefore, no strictly increasing function exists.
Statement (B) is False.
Evaluating Statement (C):
The domain \( S \) consists of 3 connected components (the intervals). The codomain \( T \) is a discrete set (in the standard topology). A continuous function mapping a connected space to a discrete space must be constant.
Thus, any continuous function \( f \) must be constant on each of the three intervals:
- \( f((0,1)) = c_1 \in T \)
- \( f((1,2)) = c_2 \in T \)
- \( f((3,4)) = c_3 \in T \)
For each interval, there are 4 choices for the constant value. Total continuous functions = \( 4 \times 4 \times 4 = 64 \).
Since \( 64 \le 120 \), this statement is correct.
Statement (C) is True.
Evaluating Statement (D):
As derived in (C), every continuous function from \( S \) to \( T \) is piecewise constant (locally constant). The derivative of a constant is 0. Thus, \( f'(x) = 0 \) for all \( x \in S \). Since the derivative exists everywhere
in the domain, the function is differentiable.
Statement (D) is True.
Correct Options: A, C, D
Option Distractor Reasons
Students may fail to apply the Pigeonhole Principle or overlook that mapping an infinite domain to a finite codomain strictly increasingly is impossible.
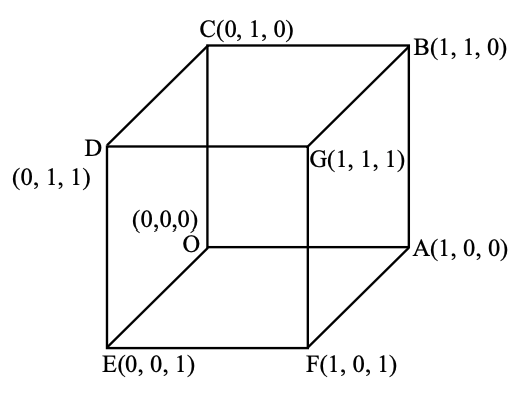 We need to find the maximum shortest distance between a line in \(S\) and a line in \(F\).
We need to find the maximum shortest distance between a line in \(S\) and a line in \(F\).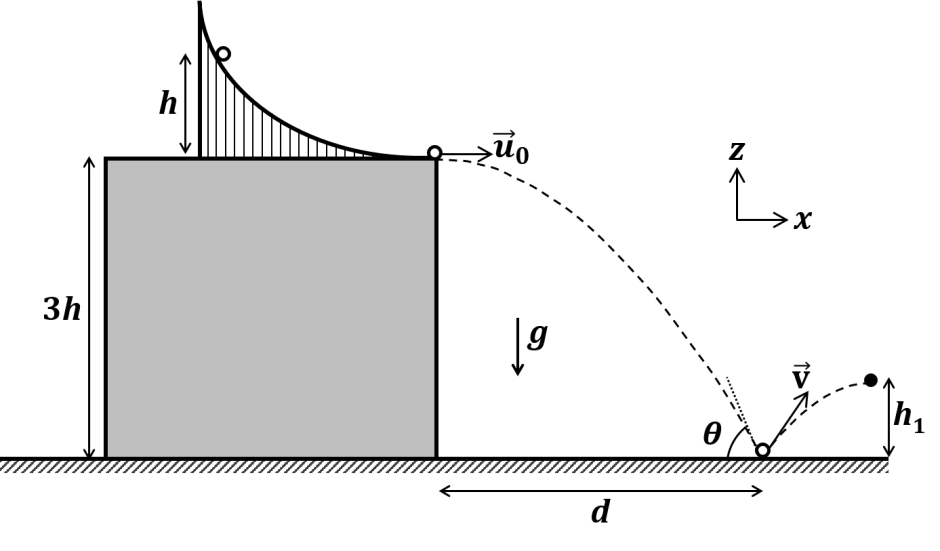




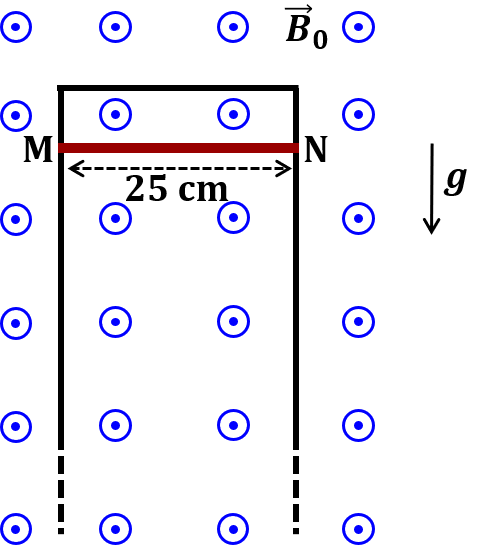
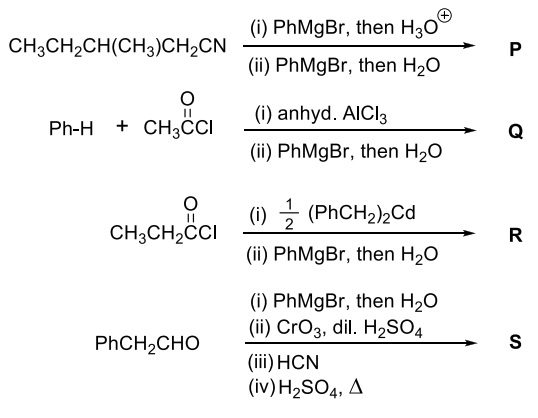
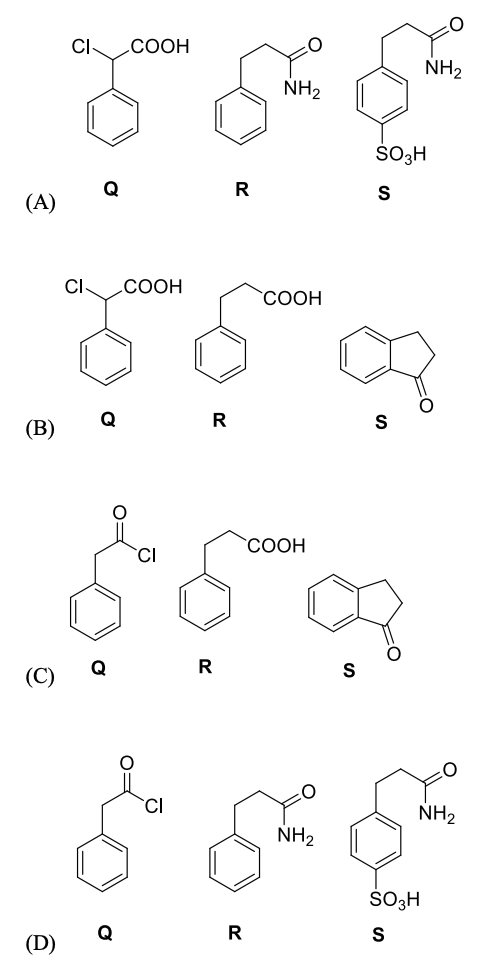
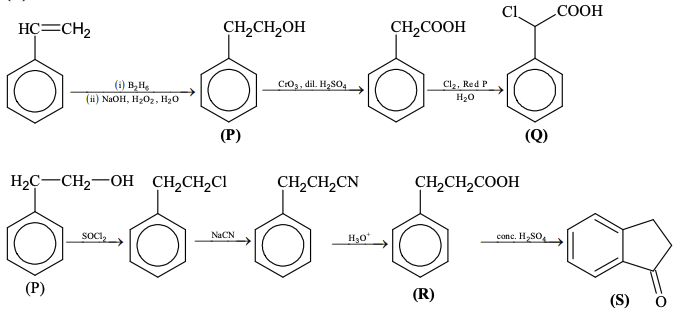
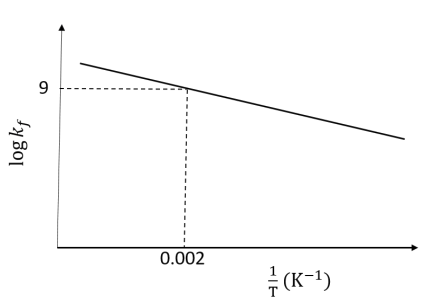 Pre-exponential factors for the forward and backward reactions are $10^{15} \text{ s}^{-1}$
and $10^{11} \text{ s}^{-1}$, respectively. If the value of $\log K$ for the reaction at 500
K is 6, the value of $|\log k_b|$ at 250 K is ___.
Pre-exponential factors for the forward and backward reactions are $10^{15} \text{ s}^{-1}$
and $10^{11} \text{ s}^{-1}$, respectively. If the value of $\log K$ for the reaction at 500
K is 6, the value of $|\log k_b|$ at 250 K is ___.
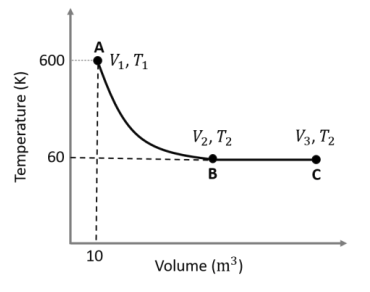 $\text{A} \to \text{B}$ is an adiabatic process. If the total heat absorbed in the entire
process ($\text{A} \to \text{B}$ and $\text{B} \to \text{C}$) is $RT_2 \ln 10$, the value of
$2 \log V_3$ is ___.
$\text{A} \to \text{B}$ is an adiabatic process. If the total heat absorbed in the entire
process ($\text{A} \to \text{B}$ and $\text{B} \to \text{C}$) is $RT_2 \ln 10$, the value of
$2 \log V_3$ is ___.
![Plot of [P] vs Time](./2023_1_English/11.png) If $T_1 = 2T_2$ and $(\Delta G^\Theta_2 - \Delta G^\Theta_1) = RT_2 \ln x$, then the value
of x is ___.
If $T_1 = 2T_2$ and $(\Delta G^\Theta_2 - \Delta G^\Theta_1) = RT_2 \ln x$, then the value
of x is ___.