JEE Advanced 2023 Paper 2 | Previous Year Questions

SECTION 1 (Maximum Marks: 12)

This section contains FOUR (04) questions.
Each question has FOUR options (A), (B), (C) and (D). ONLY ONE of these four options is the correct answer.
Full Marks: +3 If ONLY the correct option is chosen;
Zero Marks: 0 If none of the options is chosen (i.e. the question is unanswered);
Negative Marks: -1 In all other cases.

Q.1

Let $f:[1,\infty) \to \mathbb{R}$ be a differentiable function such that $f(1) = \frac{1}{3}$ and $$3 \int_{1}^{x} f(t)dt = x f(x) - \frac{x^3}{3}, \quad x \in [1,\infty).$$ Let $e$ denote the base of the natural logarithm. Then the value of $f(e)$ is

(A)

$\frac{e^2+4}{3}$

(B)

$\frac{\log_e 4 + e}{3}$

(C)

$\frac{4e^2}{3}$

(D)

$\frac{e^2-4}{3}$

(C)

Solution

Step 1: Apply Newton-Leibniz Theorem

The given integral equation is:

$$ 3\int_{1}^{x} f(t) dt = x f(x) - \frac{x^3}{3} $$

Differentiating both sides with respect to $ x $ using the Newton-Leibniz theorem:

$$ \frac{d}{dx}\left( 3\int_{1}^{x} f(t) dt \right) = \frac{d}{dx}\left( x f(x) - \frac{x^3}{3} \right) $$

$$ 3 f(x) = \left( 1 \cdot f(x) + x f'(x) \right) - x^2 $$

$$ 3 f(x) = f(x) + x f'(x) - x^2 $$

Rearranging the terms, we get:

$$ 2 f(x) = x f'(x) - x^2 $$

$$ x \frac{dy}{dx} - 2y = x^2 $$

$$ \frac{dy}{dx} - \frac{2}{x}y = x $$

This is a linear differential equation of the form $ \frac{dy}{dx} + P(x)y = Q(x) $, where $ P(x) = -\frac{2}{x} $ and $ Q(x) = x $.

Step 2: Find the Integrating Factor (I.F.)

$$ \text{I.F.} = e^{\int P(x) dx} = e^{\int -\frac{2}{x} dx} = e^{-2 \ln x} = e^{\ln(x^{-2})} = \frac{1}{x^2} $$

Step 3: Solve the Differential Equation

Multiplying the differential equation by the I.F.:

$$ y \cdot (\text{I.F.}) = \int Q(x) \cdot (\text{I.F.}) dx + C $$

$$ y \cdot \frac{1}{x^2} = \int x \cdot \frac{1}{x^2} dx + C $$

$$ \frac{y}{x^2} = \int \frac{1}{x} dx + C $$

$$ \frac{y}{x^2} = \ln x + C $$

$$ y = x^2 \ln x + C x^2 $$

Step 4: Use Initial Condition to Find C

Given $ f(1) = \frac{1}{3} $. Substituting $ x = 1 $ and $ y = 1/3 $:

$$ \frac{1}{3} = 1^2 \cdot \ln(1) + C(1)^2 $$

Since $ \ln(1) = 0 $:

$$ \frac{1}{3} = 0 + C \Rightarrow C = \frac{1}{3} $$

So, the function is:

$$ f(x) = x^2 \ln x + \frac{1}{3} x^2 $$

Step 5: Find $ f(e) $

Substitute $ x = e $:

$$ f(e) = e^2 \ln e + \frac{1}{3} e^2 $$

Since $ \ln e = 1 $:

$$ f(e) = e^2(1) + \frac{1}{3} e^2 = e^2 + \frac{e^2}{3} = \frac{4e^2}{3} $$

Correct Option: (C)

Bloom Level

Apply

Topic

Calculus

Difficulty

3

Ideal Time

120

Sub-topics

Differential Equations Newton-Leibniz Theorem Definite Integrals

PRIMARY SKILL TESTED

Solving Linear Differential Equations derived from Integral Equations

Option Distractor Reasons

A

Likely result of an algebraic error in adding terms, possibly obtaining $ \frac{e^2+4}{3} $ by miscalculating constants.

B

Incorrect integration of $ 1/x $ or logarithmic manipulation error leading to a form with $ \log_e 4 $.

D

Result of a sign error when evaluating the constant $ C $ or subtracting terms at the end.

Q.2

Consider an experiment of tossing a coin repeatedly until the outcomes of two consecutive tosses are same. If the probability of a random toss resulting in head is $\frac{1}{3}$, then the probability that the experiment stops with head is

(A)

$\frac{1}{3}$

(B)

$\frac{5}{21}$

(C)

$\frac{4}{21}$

(D)

$\frac{2}{7}$

(B)

Solution

Given:

Probability of Head $ P(H) = \frac{1}{3} $

Probability of Tail $ P(T) = 1 - \frac{1}{3} = \frac{2}{3} $

The experiment stops when two consecutive outcomes are the same (i.e., HH or TT). We need the probability that it stops with Head (i.e., ends in HH).

Analysis of Sequences:

The favorable sequences must end in HH and contain no other instances of same consecutive outcomes (like TT) before the end.

Possible favorable sequences:

HH: Probability $ \frac{1}{3} \times \frac{1}{3} = \frac{1}{9} $
THH: Probability $ \frac{2}{3} \times \frac{1}{3} \times \frac{1}{3} = \frac{2}{27} $
HTHH: Probability $ \frac{1}{3} \times \frac{2}{3} \times \frac{1}{3} \times \frac{1}{3} = \frac{2}{81} $
THTHH: Probability $ \frac{2}{3} \times \frac{1}{3} \times \frac{2}{3} \times \frac{1}{3} \times \frac{1}{3} = \frac{4}{243} $

We can group these into two infinite geometric series based on the starting outcome.

Series 1 (Starts with T, alternating until HH):

Sequences: $ THH, THTHH, THTHTHH, \dots $

First term $ a_1 = P(THH) = \frac{2}{3} \cdot \frac{1}{9} = \frac{2}{27} $

Common ratio $ r = P(HT) = \frac{1}{3} \cdot \frac{2}{3} = \frac{2}{9} $ (Every new term adds an "HT" pair before the final HH)

Sum $ S_1 = \frac{a_1}{1-r} = \frac{2/27}{1 - 2/9} = \frac{2/27}{7/9} = \frac{2}{27} \times \frac{9}{7} = \frac{2}{21} $

Series 2 (Starts with H, alternating until HH):

Sequences: $ HTHH, HTHTHH, \dots $

Note: The sequence "HH" is treated separately as the initial term.

First term $ a_2 = P(HTHH) = \frac{1}{3} \cdot \frac{2}{3} \cdot \frac{1}{9} = \frac{2}{81} $

Common ratio $ r = \frac{2}{9} $

Sum $ S_2 = \frac{a_2}{1-r} = \frac{2/81}{7/9} = \frac{2}{81} \times \frac{9}{7} = \frac{2}{63} $

Total Probability:

$$ P(E) = P(HH) + S_1 + S_2 $$

$$ P(E) = \frac{1}{9} + \frac{2}{21} + \frac{2}{63} $$

Finding a common denominator (63):

$$ P(E) = \frac{7}{63} + \frac{6}{63} + \frac{2}{63} = \frac{15}{63} $$

Simplifying the fraction:

$$ \frac{15}{63} = \frac{5}{21} $$

Correct Option: (B)

Bloom Level

Analyze

Topic

Probability

Difficulty

4

Ideal Time

150

Sub-topics

Infinite Geometric Progression Independent Events

PRIMARY SKILL TESTED

Summing infinite geometric series in a probability context

Option Distractor Reasons

A

Corresponds to the simple probability of getting a Head in a single toss, ignoring the "consecutive" condition.

C

Likely a calculation error in the summation of the geometric series, possibly missing the initial $ P(HH) $ term or one of the sub-series.

D

Another calculation error variation, possibly from incorrect common ratio determination.

Q.3

For any $y \in \mathbb{R}$, let $\cot^{-1}(y) \in (0,\pi)$ and $\tan^{-1}(y) \in (-\frac{\pi}{2}, \frac{\pi}{2})$. Then the sum of all the solutions of the equation $$\tan^{-1}\left(\frac{6y}{9-y^2}\right) + \cot^{-1}\left(\frac{9-y^2}{6y}\right) = \frac{2\pi}{3}$$ for $0 < |y| < 3$, is equal to

(A)

$2\sqrt{3}-3$

(B)

$3-2\sqrt{3}$

(C)

$4\sqrt{3}-6$

(D)

$6-4\sqrt{3}$

(C)

Solution

The given equation is:

$$ \tan^{-1}\left(\frac{6y}{9-y^2}\right) + \cot^{-1}\left(\frac{9-y^2}{6y}\right) = \frac{2\pi}{3} $$

We are given $ 0 < |y| < 3 $, which means $ y \in (-3, 0) \cup (0, 3) $.

Case 1: $ 0 < y < 3 $

In this range, the argument $ \frac{9-y^2}{6y} $ is positive.

Using the identity $ \cot^{-1}(x) = \tan^{-1}(\frac{1}{x}) $ for $ x > 0 $:

$$ \cot^{-1}\left(\frac{9-y^2}{6y}\right) = \tan^{-1}\left(\frac{6y}{9-y^2}\right) $$

Substituting this back into the equation:

$$ 2 \tan^{-1}\left(\frac{6y}{9-y^2}\right) = \frac{2\pi}{3} $$

$$ \tan^{-1}\left(\frac{6y}{9-y^2}\right) = \frac{\pi}{3} $$

$$ \frac{6y}{9-y^2} = \tan\left(\frac{\pi}{3}\right) = \sqrt{3} $$

$$ 6y = \sqrt{3}(9-y^2) $$

$$ \sqrt{3}y^2 + 6y - 9\sqrt{3} = 0 $$

Solving the quadratic equation:

$$ y = \frac{-6 \pm \sqrt{36 - 4(\sqrt{3})(-9\sqrt{3})}}{2\sqrt{3}} = \frac{-6 \pm \sqrt{36 + 108}}{2\sqrt{3}} = \frac{-6 \pm 12}{2\sqrt{3}} $$

Two solutions:

$ y_1 = \frac{6}{2\sqrt{3}} = \sqrt{3} $ (Valid as $ 0 < \sqrt{3} < 3 $)
$ y_2 = \frac{-18}{2\sqrt{3}} $ (Negative, reject for this case)

Case 2: $ -3 < y < 0 $

In this range, the argument $ x = \frac{9-y^2}{6y} $ is negative.

Using the identity $ \cot^{-1}(x) = \pi + \tan^{-1}(\frac{1}{x}) $ for $ x < 0 $:

$$ \cot^{-1}\left(\frac{9-y^2}{6y}\right) = \pi + \tan^{-1}\left(\frac{6y}{9-y^2}\right) $$

Substituting into the equation:

$$ \tan^{-1}\left(\frac{6y}{9-y^2}\right) + \pi + \tan^{-1}\left(\frac{6y}{9-y^2}\right) = \frac{2\pi}{3} $$

$$ 2 \tan^{-1}\left(\frac{6y}{9-y^2}\right) = \frac{2\pi}{3} - \pi = -\frac{\pi}{3} $$

$$ \tan^{-1}\left(\frac{6y}{9-y^2}\right) = -\frac{\pi}{6} $$

$$ \frac{6y}{9-y^2} = \tan\left(-\frac{\pi}{6}\right) = -\frac{1}{\sqrt{3}} $$

$$ 6\sqrt{3}y = -(9-y^2) $$

$$ y^2 - 6\sqrt{3}y - 9 = 0 $$

Solving for y:

$$ y = \frac{6\sqrt{3} \pm \sqrt{108 - 4(1)(-9)}}{2} = \frac{6\sqrt{3} \pm \sqrt{108+36}}{2} = \frac{6\sqrt{3} \pm 12}{2} = 3\sqrt{3} \pm 6 $$

Checking validity in $ (-3, 0) $:

$ 3\sqrt{3} + 6 $ is positive (Reject).
$ y_3 = 3\sqrt{3} - 6 $. Since $ \sqrt{3} \approx 1.732 $, $ 3(1.732) - 6 = 5.196 - 6 \approx -0.8 $. This lies in $ (-3, 0) $.

Total Sum of Solutions:

$$ \text{Sum} = y_1 + y_3 = \sqrt{3} + (3\sqrt{3} - 6) = 4\sqrt{3} - 6 $$

Correct Option: (C)

Bloom Level

Evaluate

Topic

Inverse Trigonometric Functions

Difficulty

4

Ideal Time

180

Sub-topics

Trigonometric Equations Properties of Inverse Trigonometric Functions

PRIMARY SKILL TESTED

Solving inverse trigonometric equations with domain restrictions

Option Distractor Reasons

A

Incorrectly calculating the second root or ignoring the negative domain case entirely.

B

Likely stems from sign errors when handling the identity for $ \cot^{-1}(x) $ with negative arguments.

D

Calculation error in summing the roots or solving the quadratics.

Q.4

Let the position vectors of the points $P, Q, R$ and $S$ be $\vec{a} = \hat{i} + 2\hat{j} - 5\hat{k}$, $\vec{b} = 3\hat{i} + 6\hat{j} + 3\hat{k}$, $\vec{c} = \frac{17}{5}\hat{i} + \frac{16}{5}\hat{j} + 7\hat{k}$ and $\vec{d} = 2\hat{i} + \hat{j} + \hat{k}$, respectively. Then which of the following statements is true?

(A)

The points $P, Q, R$ and $S$ are NOT coplanar

(B)

$\frac{\vec{b}+2\vec{d}}{3}$ is the position vector of a point which divides $PR$ internally in the ratio 5:4

(C)

$\frac{\vec{b}+2\vec{d}}{3}$ is the position vector of a point which divides $PR$ externally in the ratio 5:4

(D)

The square of the magnitude of the vector $\vec{b} \times \vec{d}$ is 95

(B)

Solution

Step 1: Analyze Option (A) - Coplanarity

Given points $ P(\vec{a}) $, $ Q(\vec{b}) $, $ R(\vec{c}) $, and $ S(\vec{d}) $. To check coplanarity, we check if the scalar triple product $ [\vec{PQ} \ \vec{PR} \ \vec{PS}] $ is zero.

$$ \vec{PQ} = \vec{b} - \vec{a} = 2\hat{i} + 4\hat{j} + 8\hat{k} $$

$$ \vec{PR} = \vec{c} - \vec{a} = \frac{12}{5}\hat{i} + \frac{6}{5}\hat{j} + 12\hat{k} $$

$$ \vec{PS} = \vec{d} - \vec{a} = \hat{i} - \hat{j} + 6\hat{k} $$

Calculating the determinant:

$$ \begin{vmatrix} 2 & 4 & 8 \\ 12/5 & 6/5 & 12 \\ 1 & -1 & 6 \end{vmatrix} = 2 \cdot \frac{6}{5} \begin{vmatrix} 1 & 2 & 4 \\ 2 & 1 & 10 \\ 1 & -1 & 6 \end{vmatrix} $$

Evaluating the inner determinant:

$$ 1(6 - (-10)) - 2(12 - 10) + 4(-2 - 1) = 1(16) - 2(2) + 4(-3) = 16 - 4 - 12 = 0 $$

Since the scalar triple product is 0, the points are coplanar. Thus, statement (A) is False.

Step 2: Analyze Options (B) and (C) - Section Formula

We need to identify the point given by $ \vec{v} = \frac{\vec{b} + 2\vec{d}}{3} $.

$$ \vec{v} = \frac{(3\hat{i} + 6\hat{j} + 3\hat{k}) + (4\hat{i} + 2\hat{j} + 2\hat{k})}{3} = \frac{7\hat{i} + 8\hat{j} + 5\hat{k}}{3} $$

We check if this point divides $ PR $ internally in the ratio $ 5:4 $. Using the section formula $ \frac{m\vec{c} + n\vec{a}}{m+n} $ with $ m=5, n=4 $:

$$ \text{Point} = \frac{5\vec{c} + 4\vec{a}}{9} = \frac{5(\frac{17}{5}\hat{i} + \frac{16}{5}\hat{j} + 7\hat{k}) + 4(\hat{i} + 2\hat{j} - 5\hat{k})}{9} $$

$$ = \frac{(17\hat{i} + 16\hat{j} + 35\hat{k}) + (4\hat{i} + 8\hat{j} - 20\hat{k})}{9} $$

$$ = \frac{21\hat{i} + 24\hat{j} + 15\hat{k}}{9} = \frac{3(7\hat{i} + 8\hat{j} + 5\hat{k})}{9} = \frac{7\hat{i} + 8\hat{j} + 5\hat{k}}{3} $$

This matches $ \vec{v} $. Therefore, the point divides $ PR $ internally in the ratio $ 5:4 $. Statement (B) is True.

Step 3: Analyze Option (D)

$$ \vec{b} \times \vec{d} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 3 & 6 & 3 \\ 2 & 1 & 1 \end{vmatrix} = \hat{i}(3) - \hat{j}(-3) + \hat{k}(-9) = 3\hat{i} + 3\hat{j} - 9\hat{k} $$

$$ |\vec{b} \times \vec{d}|^2 = 3^2 + 3^2 + (-9)^2 = 9 + 9 + 81 = 99 $$

Since $ 99 \neq 95 $, statement (D) is False.

Bloom Level

Apply

Topic

Vectors

Difficulty

3

Ideal Time

150

Sub-topics

Section Formula Scalar Triple Product Vector Product

PRIMARY SKILL TESTED

Application of vector section formula and checking coplanarity

Option Distractor Reasons

A

Calculation error in the scalar triple product leading to a non-zero value, falsely suggesting points are not coplanar.

C

Confusing the formula for internal and external division.

D

Arithmetic mistake when calculating the square of the magnitude of the cross product.

SECTION 2 (Maximum Marks: 12)

This section contains THREE (03) questions.
Each question has FOUR options (A), (B), (C) and (D). ONE OR MORE THAN ONE of these four option(s) is (are) correct answer(s).
Full Marks: +4 ONLY if (all) the correct option(s) is(are) chosen;
Partial Marks: +3 If all the four options are correct but ONLY three options are chosen;
Partial Marks: +2 If three or more options are correct but ONLY two options are chosen, both of which are correct;
Partial Marks: +1 If two or more options are correct but ONLY one option is chosen and it is a correct option;
Negative Marks: -2 In all other cases.

Q.5

Let $M = (a_{ij}), i,j \in \{1,2,3\}$, be the $3 \times 3$ matrix such that $a_{ij} = 1$ if $j+1$ is divisible by $i$, otherwise $a_{ij} = 0$. Then which of the following statements is(are) true?

(A)

$M$ is invertible

(B)

There exists a nonzero column matrix $\begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix}$ such that $M \begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix} = \begin{pmatrix} -a_1 \\ -a_2 \\ -a_3 \end{pmatrix}$

(C)

The set $\{X \in \mathbb{R}^3 : MX = \mathbf{0}\} \neq \{\mathbf{0}\}$, where $\mathbf{0} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}$

(D)

The matrix $(M-2I)$ is invertible, where $I$ is the $3 \times 3$ identity matrix

(B), (C)

Solution

Step 1: Construct Matrix M

The condition is $ a_{ij} = 1 $ if $ j+1 $ is divisible by $ i $, otherwise 0.

Row 1 ($i=1$): $ j+1 $ is always divisible by 1. So, $ [1, 1, 1] $.
Row 2 ($i=2$):
- $ j=1 \Rightarrow j+1=2 $ (Divisible by 2) $\rightarrow 1$
- $ j=2 \Rightarrow j+1=3 $ (Not divisible) $\rightarrow 0$
- $ j=3 \Rightarrow j+1=4 $ (Divisible by 2) $\rightarrow 1$
- Row: $ [1, 0, 1] $
Row 3 ($i=3$):
- $ j=1 \Rightarrow j+1=2 $ (Not divisible) $\rightarrow 0$
- $ j=2 \Rightarrow j+1=3 $ (Divisible by 3) $\rightarrow 1$
- $ j=3 \Rightarrow j+1=4 $ (Not divisible) $\rightarrow 0$
- Row: $ [0, 1, 0] $

$$ M = \begin{bmatrix} 1 & 1 & 1 \\ 1 & 0 & 1 \\ 0 & 1 & 0 \end{bmatrix} $$

Step 2: Check Option (A) - Invertibility

Calculate determinant $ |M| $:

$$ |M| = 1(0-1) - 1(0-0) + 1(1-0) = -1 - 0 + 1 = 0 $$

Since $ |M| = 0 $, M is not invertible. (A) is False.

Step 3: Check Option (B)

We test if there exists a non-zero vector $ X $ such that $ MX = -X $, or $ (M+I)X = 0 $.

$$ M+I = \begin{bmatrix} 2 & 1 & 1 \\ 1 & 1 & 1 \\ 0 & 1 & 1 \end{bmatrix} $$

Solving $ (M+I)X = 0 $:

$ R_1 \rightarrow R_1 - R_2 $: $ \begin{bmatrix} 1 & 0 & 0 \end{bmatrix} \Rightarrow x_1 = 0 $.

From $ R_3 $: $ x_2 + x_3 = 0 \Rightarrow x_2 = -x_3 $.

Let $ x_3 = k \neq 0 $, then $ X = [0, -k, k]^T $. This is a non-zero column matrix. (B) is True.

Step 4: Check Option (C)

The set $ \{X \in \mathbb{R}^3 : MX = 0\} $ is the null space. Since $ |M| = 0 $, the null space contains non-zero vectors. So the set is not just $ \{0\} $. (C) is True.

Step 5: Check Option (D)

Calculate $ |M - 2I| $:

$$ M - 2I = \begin{bmatrix} -1 & 1 & 1 \\ 1 & -2 & 1 \\ 0 & 1 & -2 \end{bmatrix} $$

$$ |M-2I| = -1(4-1) - 1(-2-0) + 1(1-0) = -3 + 2 + 1 = 0 $$

Since the determinant is 0, $ M-2I $ is not invertible. (D) is False.

Correct Statements: (B) and (C)

Bloom Level

Analyze

Topic

Matrices

Difficulty

3

Ideal Time

180

Sub-topics

Determinants Homogeneous Linear Equations Eigenvalues

PRIMARY SKILL TESTED

Constructing matrices based on rules and analyzing their invertibility and null space

Option Distractor Reasons

A

Calculation error in finding the determinant of M, leading the student to believe it is non-zero.

D

Incorrectly calculating the determinant of (M-2I) or assuming invertibility without checking.

Q.6

Let $f:(0,1) \to \mathbb{R}$ be the function defined as $f(x) = [4x](x-\frac{1}{4})^2(x-\frac{1}{2})$, where $[x]$ denotes the greatest integer less than or equal to $x$. Then which of the following statements is(are) true?

(A)

The function $f$ is discontinuous exactly at one point in $(0,1)$

(B)

There is exactly one point in $(0,1)$ at which the function $f$ is continuous but NOT differentiable

(C)

The function $f$ is NOT differentiable at more than three points in $(0,1)$

(D)

The minimum value of the function $f$ is $-\frac{1}{512}$

(A), (B)

Solution

Function Definition:

$$ f(x) = [4x] \left(x - \frac{1}{4}\right)^2 \left(x - \frac{1}{2}\right) $$

We analyze the function in sub-intervals of $ (0, 1) $ based on values of $ [4x] $:

$ 0 < x < \frac{1}{4} \Rightarrow [4x]=0 \Rightarrow f(x)=0 $
$ \frac{1}{4} \le x < \frac{1}{2} \Rightarrow [4x] = 1 \Rightarrow f(x) = \left(x - \frac{1}{4}\right)^2 \left(x - \frac{1}{2}\right) $
$ \frac{1}{2} \le x < \frac{3}{4} \Rightarrow [4x]=2 \Rightarrow f(x)=2 \left(x - \frac{1}{4}\right)^2 \left(x - \frac{1}{2}\right) $
$ \frac{3}{4} \le x < 1 \Rightarrow [4x]=3 \Rightarrow f(x)=3 \left(x - \frac{1}{4}\right)^2 \left(x - \frac{1}{2}\right) $

Step 1: Check Continuity

Potential discontinuities are at $ x = \frac{1}{4}, \frac{1}{2}, \frac{3}{4} $.

At $ x = 1/4 $: LHL = 0. RHL = $ 1(0)^2(...) = 0 $. Continuous.
At $ x = 1/2 $: LHL = $ 1(...)(0) = 0 $. RHL = $ 2(...)(0) = 0 $. Continuous.
At $ x = 3/4 $:
- LHL = $ 2(3/4 - 1/4)^2(3/4 - 1/2) = 2(1/2)^2(1/4) = 2(1/4)(1/4) = \frac{1}{8} $.
- RHL = $ 3(3/4 - 1/4)^2(3/4 - 1/2) = 3(1/2)^2(1/4) = \frac{3}{16} $.
- $ \text{LHL} \neq \text{RHL} $. Discontinuous.

Thus, $ f $ is discontinuous exactly at one point ($x = 3/4$). (A) is True.

Step 2: Check Differentiability

At $ x = 1/4 $: $ f'(1/4^-) = 0 $. For $ x > 1/4 $, derivative has a factor of $ (x-1/4) $, so $ f'(1/4^+) = 0 $. Differentiable.
At $ x = 1/2 $:
- LHD (using $ 1 \cdot (... ) $): $ \frac{d}{dx}[(x-1/4)^2(x-1/2)]|_{x=1/2} = (x-1/4)^2(1) + 2(x-1/4)(x-1/2)|_{1/2} = (1/4)^2 = \frac{1}{16} $.
- RHD (using $ 2 \cdot (... ) $): $ 2 \times (\text{derivative of inner part}) = 2 \times \frac{1}{16} = \frac{1}{8} $.
- $ 1/16 \neq 1/8 $. Not Differentiable.
At $ x = 3/4 $: Discontinuous, so Not Differentiable.

The function is continuous but not differentiable exactly at one point ($ x = 1/2 $). (B) is True.

Step 3: Minimum Value

In $ (0, 1/4) $, $ f(x) = 0 $.

In $ (1/4, 1/2) $, $ f(x) = (x-1/4)^2(x-1/2) $. Since $ x < 1/2 $, this value is negative. The global minimum must lie here.

Let $ g(x) = (x-1/4)^2(x-1/2) $. Differentiating:

$$ g'(x) = 2(x-1/4)(x-1/2) + (x-1/4)^2 = (x-1/4)[2x - 1 + x - 1/4] = (x-1/4)(3x - 5/4) $$

Critical point at $ x = 5/12 $. Value:

$$ g(5/12) = (5/12 - 3/12)^2 (5/12 - 6/12) = (2/12)^2 (-1/12) = \frac{1}{36} \cdot \left(-\frac{1}{12}\right) = -\frac{1}{432} $$

Option (D) claims $ -1/512 $, which is incorrect.

Correct Statements: (A) and (B)

Bloom Level

Analyze

Topic

Calculus

Difficulty

4

Ideal Time

200

Sub-topics

Continuity and Differentiability Greatest Integer Function Maxima and Minima

PRIMARY SKILL TESTED

Analyzing continuity and differentiability of piecewise functions involving floor functions

Option Distractor Reasons

C

Counting points of non-differentiability incorrectly (e.g., including x=1/4 or missing x=3/4).

D

Arithmetic error during the calculation of the local minimum value (e.g., calculating -1/512 instead of -1/432).

Q.7

Let $S$ be the set of all twice differentiable functions $f$ from $\mathbb{R}$ to $\mathbb{R}$ such that $\frac{d^2f}{dx^2}(x) > 0$ for all $x \in (-1,1)$. For $f \in S$, let $X_f$ be the number of points $x \in (-1,1)$ for which $f(x) = x$. Then which of the following statements is(are) true?

(A)

There exists a function $f \in S$ such that $X_f = 0$

(B)

For every function $f \in S$, we have $X_f \leq 2$

(C)

There exists a function $f \in S$ such that $X_f = 2$

(D)

There does NOT exist any function $f$ in $S$ such that $X_f = 1$

(A), (B), (C)

Solution

Step 1: Analyze the geometric properties of $ f(x) $

The condition $ \frac{d^2f}{dx^2}(x) > 0 $ for all $ x \in (-1, 1) $ implies that the function $ f(x) $ is strictly concave upward (convex) in this interval.

We are interested in the number of solutions to $ f(x) = x $ in the interval $ (-1, 1) $. This is equivalent to finding the number of intersection points between the curve $ y = f(x) $ and the line $ y = x $.

Step 2: Analyze the possible number of intersections

A strictly convex curve can intersect a straight line at most at 2 points. Let's consider examples for different cases:

Case $ X_f = 0 $: The curve lies completely above or below the line without touching.
Example: Let $ f(x) = x^2 + 2 $. Since $ x^2 - x + 2 = 0 $ has a negative discriminant, there are no real solutions. Thus, $ X_f = 0 $ is possible. (Statement A is True)
Case $ X_f = 1 $: The line is tangent to the curve or crosses it exactly once in the domain.
Example: Let $ f(x) = x^2 + \frac{1}{4} $. Solving $ x^2 + \frac{1}{4} = x $ gives $ (x - \frac{1}{2})^2 = 0 $, so $ x = \frac{1}{2} $. Since $ \frac{1}{2} \in (-1, 1) $, $ X_f = 1 $ is possible. (Statement D is False)
Case $ X_f = 2 $: The line acts as a secant line crossing the curve twice.
Example: Let $ f(x) = 2x^2 $. Solving $ 2x^2 = x $ gives $ x(2x - 1) = 0 $, so $ x = 0 $ and $ x = \frac{1}{2} $. Both are in $ (-1, 1) $. Thus, $ X_f = 2 $ is possible. (Statement C is True)

Since a line cannot intersect a strictly convex curve at more than 2 points, $ X_f \le 2 $ always holds. (Statement B is True)

Correct Options: (A), (B), (C)

Bloom Level

Analyze

Topic

Calculus

Difficulty

3

Ideal Time

90

Sub-topics

Concavity Intersection of Curves

PRIMARY SKILL TESTED

Geometric interpretation of the second derivative

Option Distractor Reasons

D

The student may overlook the possibility of the line $ y = x $ being tangent to the curve, which results in exactly one intersection point.

SECTION 3 (Maximum Marks: 24)

This section contains SIX (06) questions.
The answer to each question is a NON-NEGATIVE INTEGER.
Full Marks: +4 If ONLY the correct integer is entered;
Zero Marks: 0 In all other cases.

Q.8

For $x \in \mathbb{R}$, let $\tan^{-1}(x) \in (-\frac{\pi}{2}, \frac{\pi}{2})$. Then the minimum value of the function $$f: \mathbb{R} \to \mathbb{R} \text{ defined by } f(x) = \int_{0}^{x \tan^{-1} x} \frac{e^{(t-\cos t)}}{1+t^{2023}} dt \text{ is}$$

0

Solution

Step 1: Apply Leibniz Rule for differentiation of integrals

Given function: $$ f(x) = \int_{0}^{x \tan^{-1} x} \frac{e^{(t-\cos t)}}{1+t^{2023}} dt $$

Differentiating with respect to $ x $: $$ f'(x) = \frac{e^{(x \tan^{-1} x - \cos(x \tan^{-1} x))}}{1+(x \tan^{-1} x)^{2023}} \cdot \frac{d}{dx}(x \tan^{-1} x) - 0 $$

Since $ e^y > 0 $ and the denominator $ 1 + t^{2023} > 0 $ for $ t \ge 0 $ (note that $ x \tan^{-1} x \ge 0 $ for all real $ x $), the term containing the exponential is always positive.

The sign of $ f'(x) $ depends entirely on the derivative of the upper limit, $ g(x) = x \tan^{-1} x $.

Step 2: Analyze the derivative

$$ \frac{d}{dx}(x \tan^{-1} x) = \tan^{-1} x + \frac{x}{1+x^2} $$

Let $ h(x) = \tan^{-1} x + \frac{x}{1+x^2} $.

If $ x > 0 $, $ \tan^{-1} x > 0 $ and $ \frac{x}{1+x^2} > 0 $, so $ h(x) > 0 $.
If $ x < 0 $, $ \tan^{-1} x < 0 $ and $ \frac{x}{1+x^2} < 0 $, so $ h(x) < 0 $.
If $ x = 0 $, $ h(x) = 0 $.

Thus, $ f'(x) < 0 $ for $ x < 0 $ and $ f '(x) > 0 $ for $ x > 0 $. This implies that $ f(x) $ decreases until $ x = 0 $ and increases afterwards.

Step 3: Find the minimum value

The global minimum occurs at $ x = 0 $.

Substitute $ x = 0 $ into the original function:

$$ f(0) = \int_{0}^{0 \cdot \tan^{-1} 0} \dots dt = \int_{0}^{0} \dots dt = 0 $$

Answer: 0

Bloom Level

Apply

Topic

Calculus

Difficulty

3

Ideal Time

120

Sub-topics

Leibniz Rule Definite Integrals Maxima and Minima

PRIMARY SKILL TESTED

Minimizing a function defined by an integral

Q.9

For $x \in \mathbb{R}$, let $y(x)$ be a solution of the differential equation $$(x^2-5)\frac{dy}{dx} - 2xy = -2x(x^2-5)^2 \text{ such that } y(2) = 7.$$ Then the maximum value of the function $y(x)$ is

16

Solution

Step 1: Write in Linear Differential Equation Form

The given equation is:

$$ (x^2 - 5)\frac{dy}{dx} - 2xy = -2x(x^2 - 5)^2 $$

Dividing by $ x^2 - 5 $:

$$ \frac{dy}{dx} - \frac{2x}{x^2 - 5}y = -2x(x^2 - 5) $$

This is of the form $ \frac{dy}{dx} + P(x)y = Q(x) $, where $ P(x) = -\frac{2x}{x^2 - 5} $ and $ Q(x) = -2x(x^2 - 5) $.

Step 2: Find the Integrating Factor (I.F.)

$$ \text{I.F.} = e^{\int P(x) dx} = e^{\int -\frac{2x}{x^2 - 5} dx} = e^{-\ln|x^2 - 5|} = \frac{1}{x^2 - 5} $$

Step 3: Solve the Equation

Multiply the DE by the I.F.:

$$ y \cdot \frac{1}{x^2 - 5} = \int Q(x) \cdot \text{I.F.} \, dx $$

$$ \frac{y}{x^2 - 5} = \int -2x(x^2 - 5) \cdot \frac{1}{x^2 - 5} \, dx $$

$$ \frac{y}{x^2 - 5} = \int -2x \, dx = -x^2 + C $$

So, the general solution is:

$$ y = (x^2 - 5)(C - x^2) $$

Step 4: Use Initial Condition

Given $ y(2) = 7 $. Substitute $ x = 2, y = 7 $:

$$ 7 = (2^2 - 5)(C - 2^2) $$

$$ 7 = (4 - 5)(C - 4) $$

$$ 7 = -1(C - 4) \Rightarrow -7 = C - 4 \Rightarrow C = -3 $$

Thus, the function is:

$$ y(x) = (x^2 - 5)(-3 - x^2) = -(x^2 - 5)(x^2 + 3) $$

$$ y(x) = -(x^4 - 2x^2 - 15) = -x^4 + 2x^2 + 15 $$

Step 5: Find the Maximum Value

Let $ t = x^2 $, where $ t \ge 0 $. The function becomes $ g(t) = -t^2 + 2t + 15 $.

This is a downward opening parabola. The maximum occurs at the vertex:

$$ t = \frac{-b}{2a} = \frac{-2}{2(-1)} = 1 $$

Since $ t = 1 $ corresponds to $ x = \pm 1 $ (which is within the valid domain for continuity near the initial point), the maximum value is:

$$ g(1) = -(1)^2 + 2(1) + 15 = 16 $$

Answer: 16

Bloom Level

Apply

Topic

Differential Equations

Difficulty

3

Ideal Time

150

Sub-topics

Linear Differential Equations Quadratic Optimization

PRIMARY SKILL TESTED

Solving first-order linear DEs

Q.10

Let $X$ be the set of all five digit numbers formed using 1,2,2,2,4,4,0. For example, 22240 is in $X$ while 02244 and 44422 are not in $X$. Suppose that each element of $X$ has an equal chance of being chosen. Let $p$ be the conditional probability that an element chosen at random is a multiple of 20 given that it is a multiple of 5. Then the value of $38p$ is equal to

31

Solution

Step 1: Understand the sample space and available digits

The set of digits available is $ D = \{1, 2, 2, 2, 4, 4, 0\} $. We are forming 5-digit numbers. Note that 0 cannot be the first digit, but since we are selecting a subset of 5 digits from D, we must first determine the valid combinations.

Step 2: Calculate $ n(A) $ (Number of elements divisible by 5)

Let $ A $ be the event that the number is a multiple of 5. For a number to be divisible by 5, it must end in 0 or 5. Since 5 is not in $ D $, the number must end in 0.

Since the number ends in 0, the digit 0 is used. We need to choose 4 more digits from the remaining set $ \{1, 2, 2, 2, 4, 4\} $ and arrange them in the first 4 positions.

We enumerate the possible sets of 4 digits and their permutations:

{2, 2, 2, 4}: Permutations = $ \frac{4!}{3!1!} = 4 $
{2, 2, 4, 4}: Permutations = $ \frac{4!}{2!2!} = 6 $
{1, 2, 2, 2}: Permutations = $ \frac{4!}{1!3!} = 4 $
{1, 2, 2, 4}: Permutations = $ \frac{4!}{1!2!1!} = 12 $
{1, 2, 4, 4}: Permutations = $ \frac{4!}{1!1!2!} = 12 $

Total numbers in $ A $: $ n(A) = 4 + 6 + 4 + 12 + 12 = 38 $.

Step 3: Calculate $ n(B) $ (Number of elements divisible by 20)

Let $ B $ be the event that the number is divisible by 20 (and thus by 5, so $ B \subset A $). A number is divisible by 20 if it is divisible by 5 and 4. It must end in 0, and the last two digits must form a number divisible by 20. With the available digits, the last two digits can be 20 or 40.

Case B1: Ends in 20

Digits used: {2, 0}. Remaining to choose: 3 digits from $ \{1, 2, 2, 4, 4\} $.

{1, 2, 2}: Permutations = $ \frac{3!}{1!2!} = 3 $
{1, 2, 4}: Permutations = $ 3! = 6 $
{1, 4, 4}: Permutations = $ \frac{3!}{1!2!} = 3 $
{2, 2, 4}: Permutations = $ \frac{3!}{2!1!} = 3 $
{2, 4, 4}: Permutations = $ \frac{3!}{1!2!} = 3 $

Total for B1 = $ 3 + 6 + 3 + 3 + 3 = 18 $.

Case B2: Ends in 40

Digits used: {4, 0}. Remaining to choose: 3 digits from $ \{1, 2, 2, 2, 4\} $.

{1, 2, 2}: Permutations = $ \frac{3!}{1!2!} = 3 $
{1, 2, 4}: Permutations = $ 3! = 6 $
{2, 2, 2}: Permutations = $ \frac{3!}{3!} = 1 $
{2, 2, 4}: Permutations = $ \frac{3!}{2!1!} = 3 $

Total for B2 = $ 3 + 6 + 1 + 3 = 13 $.

Total $ n(B) = 18 + 13 = 31 $.

Step 4: Calculate Conditional Probability and Final Value

The conditional probability $ p = P(B|A) = \frac{n(A \cap B)}{n(A)} $.

Since all numbers divisible by 20 are divisible by 5, $ A \cap B = B $.

$$ p = \frac{31}{38} $$

We are asked for the value of $ 38p $:

$$ 38p = 38 \times \frac{31}{38} = 31 $$

Answer: 31

Bloom Level

Analyze

Topic

Probability

Difficulty

4

Ideal Time

240

Sub-topics

Conditional Probability Permutations with Repetition

PRIMARY SKILL TESTED

Enumerating permutations of subsets from a multiset under constraints

Q.11

Let $A_1, A_2, A_3, \dots, A_8$ be the vertices of a regular octagon that lie on a circle of radius 2. Let $P$ be a point on the circle and let $PA_i$ denote the distance between the points $P$ and $A_i$ for $i = 1, 2, \dots, 8$. If $P$ varies over the circle, then the maximum value of the product $PA_1 \cdot PA_2 \cdot \dots \cdot PA_8$, is

512

Solution

Step 1: Formulate the problem using Complex Numbers

Let the circle be the set of points $ z $ in the complex plane such that $ |z| = 2 $. The vertices of the regular octagon $ A_1, A_2, \dots, A_8 $ can be represented as the roots of the equation $ z^8 = 2^8 $.

The polynomial whose roots are the vertices $ A_k $ is $ Q(z) = z^8 - 2^8 $.

Step 2: Express the product of distances

Let the point $ P $ on the circle be represented by the complex number $ z $. The distance $ PA_k $ is given by $ |z - A_k| $.

The product of the distances is:

$$ \prod_{k=1}^{8} PA_k = \prod_{k=1}^{8} |z - A_k| = \left| \prod_{k=1}^{8} (z - A_k) \right| $$

Since $ A_k $ are the roots of $ z^8 - 2^8 $, the product $ \prod (z - A_k) $ is simply the polynomial evaluated at $ z $:

$$ \prod_{k=1}^{8} PA_k = |z^8 - 2^8| $$

Step 3: Maximize the expression

Since $ P $ lies on the circle of radius 2, we can write $ z = 2e^{i\theta} $. Substituting this into the expression:

$$ |z^8 - 2^8| = |(2e^{i\theta})^8 - 2^8| = |2^8 e^{i8\theta} - 2^8| $$

Factor out $ 2^8 $:

$$ = 2^8 |e^{i8\theta} - 1| $$

Using Euler's formula or geometry, the maximum value of $ |e^{i\phi} - 1| $ (the distance between a point on the unit circle and 1) is 2, which occurs when $ e^{i\phi}=- 1 $ (i.e., $ \phi=\ pi, 3\pi, \dots $).

Here $ \phi = 8\theta $. As $ P $ varies over the circle, $ \theta $ varies, so $ 8\theta $ can take any value.

Therefore, the maximum value is:

$$ 2^8 \times 2 = 2^9 = 512 $$

Answer: 512

Bloom Level

Apply

Topic

Complex Numbers

Difficulty

3

Ideal Time

180

Sub-topics

Geometry of Complex Numbers Roots of Unity

PRIMARY SKILL TESTED

Using polynomial factorization properties of roots of unity to calculate distances

Q.12

Let $$R = \left\{ \begin{pmatrix} a & 3 & b \\ c & 2 & d \\ 0 & 5 & 0 \end{pmatrix} : a,b,c,d \in \{0,3,5,7,11,13,17,19\} \right\}.$$ Then the number of invertible matrices in $R$ is

3780

Solution

Step 1: Total Number of Matrices

The set of allowed values is $ S = \{0, 3, 5, 7, 11, 13, 17, 19\} $. This set contains 0 and 7 prime numbers. Total size $ |S| = 8 $.

The matrix is $ M = \begin{pmatrix} a & 3 & b \\ c & 2 & d \\ 0 & 5 & 0 \end{pmatrix} $.

There are 4 variable entries: $ a, b, c, d $. Each can be chosen in 8 ways.

$$ \text{Total matrices} = 8^4 = (2^3)^4 = 2^{12} = 4096 $$

Step 2: Condition for Non-Invertibility

The determinant of M is found by expanding along the 3rd row:

$$ |M| = -5(ad - bc) = 5(bc - ad) $$

For the matrix to be non-invertible (singular), $ |M| = 0 $, which implies $ ad = bc $.

We need to count the number of quadruplets $ (a,b,c,d) $ from $ S $ such that $ ad = bc $.

Step 3: Counting Non-Invertible Cases

Let $ P = \{3, 5, 7, 11, 13, 17, 19\} $ be the set of non-zero elements (all are primes).

Case I: Non-zero Product ($ ad = bc \neq 0 $)

Here $ a, b, c, d \in P $. Since the elements are prime, unique factorization applies.

If $ ad = bc $, then the multiset of factors must be identical: $ \{a, d\} = \{b, c\} $.

Subcase A: $ a $ and $ d $ are distinct primes.
- We choose 2 distinct primes from P: $ \binom{7}{2} = 21 $ ways.
- Let the primes be $ x, y $. So $ \{a,d\} = \{x,y\} $. There are 2 permutations ($ a=x, d=y $ or $ a=y, d=x $).
- Consequently, $ \{b,c\} = \{x,y\} $. There are 2 permutations.
- Total ways = $ 21 \times 2 \times 2 = 84 $.
Subcase B: $ a $ and $ d $ are the same prime.
- We choose 1 prime from P: $ \binom{7}{1} = 7 $ ways.
- Let the prime be $ x $. So $ a=x, d=x $. Only 1 permutation.
- Consequently, $ b=x, c=x $. Only 1 permutation.
- Total ways = $ 7 \times 1 \times 1 = 7 $.

Total for Case I = $ 84 + 7 = 91 $.

Case II: Zero Product ($ ad = bc = 0 $)

For $ ad = 0 $, at least one of $ a, d $ must be 0. Total pairs $ (a,d) $ is $ 8 \times 8 = 64 $. Pairs with no zero is $ 7 \times 7 = 49 $. So pairs with at least one zero is $ 64 - 49 = 15 $.

Similarly, for $ bc = 0 $, there are 15 pairs.

Since the choices for $ (a,d) $ and $ (b,c) $ are independent:

Total for Case II = $ 15 \times 15 = 225 $.

Step 4: Calculate Invertible Matrices

Total Non-Invertible Matrices = $ 91 + 225 = 316 $.

Number of Invertible Matrices = Total - Non-Invertible

$$ = 4096 - 316 = 3780 $$

Answer: 3780

Bloom Level

Analyze

Topic

Matrices

Difficulty

4

Ideal Time

240

Sub-topics

Determinants Combinatorics Prime Number Properties

PRIMARY SKILL TESTED

Counting combinations of matrix elements to satisfy a determinant condition

Q.13

Let $C_1$ be the circle of radius 1 with center at the origin. Let $C_2$ be the circle of radius $r$ with center at the point $A = (4,1)$, where $1 < r < 3$. Two distinct common tangents $PQ$ and $ST$ of $C_1$ and $C_2$ are drawn. The tangent $PQ$ touches $C_1$ at $P$ and $C_2$ at $Q$. The tangent $ST$ touches $C_1$ at $S$ and $C_2$ at $T$. Mid points of the line segments $PQ$ and $ST$ are joined to form a line which meets the $x$-axis at a point $B$. If $AB=\sqrt{5}$, then the value of $r^2$ is

2

Solution

Step 1: Identify the Equations of the Circles

Let the first circle $ C_1 $ be $ S_1 = 0 $:

$$ x^2 + y^2 - 1 = 0 $$

Center $ O(0, 0) $, Radius $ R_1 = 1 $.

Let the second circle $ C_2 $ be $ S_2 = 0 $:

$$ (x-4)^2 + (y-1)^2 - r^2 = 0 $$

$$ x^2 + y^2 - 8x - 2y + 17 - r^2 = 0 $$

Center $ A(4, 1) $, Radius $ R_2 = r $.

Step 2: Use the Radical Axis Property

The line joining the midpoints of the common tangents ($PQ$ and $ST$) to two circles is their Radical Axis.

The equation of the radical axis is given by $ S_1 - S_2 = 0 $:

$$ (x^2 + y^2 - 1) - (x^2 + y^2 - 8x - 2y + 17 - r^2) = 0 $$

$$ 8x + 2y - 18 + r^2 = 0 $$

Step 3: Find the coordinates of point B

The line meets the x-axis at point $ B $. For the x-axis, $ y = 0 $.

$$ 8x - 18 + r^2 = 0 \Rightarrow x = \frac{18 - r^2}{8} $$

So, the coordinates of $ B $ are $ \left( \frac{18 - r^2}{8}, 0 \right) $.

Step 4: Use the distance AB

We are given $ AB = \sqrt{5} $, where $ A = (4, 1) $. Using the distance formula:

$$ AB^2 = 5 $$

$$ \left( 4 - \frac{18 - r^2}{8} \right)^2 + (1 - 0)^2 = 5 $$

$$ \left( \frac{32 - (18 - r^2)}{8} \right)^2 + 1 = 5 $$

$$ \left( \frac{14 + r^2}{8} \right)^2 = 4 $$

Taking the square root:

$$ \frac{14 + r^2}{8} = \pm 2 $$

Case 1: $ \frac{14 + r^2}{8} = 2 \Rightarrow 14 + r^2 = 16 \Rightarrow r^2 = 2 $.

Case 2: $ \frac{14 + r^2}{8} = -2 \Rightarrow 14 + r^2 = -16 \Rightarrow r^2 = -30 $ (Not possible as $ r^2 \ge 0 $).

Thus, $ r^2 = 2 $.

Bloom Level

Apply

Topic

Coordinate Geometry

Difficulty

3

Ideal Time

120

Sub-topics

Radical Axis Circles Common Tangents

PRIMARY SKILL TESTED

Applying the property of the radical axis relative to common tangents

SECTION 4 (Maximum Marks: 12)

This section contains TWO (02) paragraphs.
Based on each paragraph, there are TWO (02) questions.
The answer to each question is a NUMERICAL VALUE.
If the numerical value has more than two decimal places, truncate/round-off the value to TWO decimal places.
Full Marks: +3 If ONLY the correct numerical value is entered;
Zero Marks: 0 In all other cases.

PARAGRAPH "I"

Consider an obtuse angled triangle $ABC$ in which the difference between the largest and the smallest angle is $\frac{\pi}{2}$ and whose sides are in arithmetic progression. Suppose that the vertices of this triangle lie on a circle of radius 1.

Q.14

Let $a$ be the area of the triangle $ABC$. Then the value of $(64a)^2$ is

1008

Solution

Step 1: Formulate trigonometric relations

Given an obtuse triangle $ ABC $ with angles $ A > B > C $. Let $ A $ be the obtuse angle.

1. Difference condition: $ A - C = \frac{\pi}{2} \Rightarrow A = \frac{\pi}{2} + C $.

2. AP condition for sides: $ a, b, c $ are in A.P. $ \Rightarrow 2b = a + c $.

Using the Sine Rule (and $ R=1 $): $ b = 2R\sin B, a = 2R\sin A, c = 2R\sin C $. $$ 2\sin B = \sin A + \sin C $$

3. Sum of angles: $ A + B + C = \pi $.

Substituting $ A $: $ (\frac{\pi}{2} + C) + B + C = \pi \Rightarrow B + 2C = \frac{\pi}{2} \Rightarrow B = \frac{\pi}{2} - 2C $.

Step 2: Solve for angle C

Substitute $ A $ and $ B $ into the sine relation:

$$ 2\sin(\frac{\pi}{2} - 2C) = \sin(\frac{\pi}{2} + C) + \sin C $$

$$ 2\cos 2C = \cos C + \sin C $$

Use double angle identity: $ 2(\cos^2 C - \sin^2 C) = \cos C + \sin C $.

$$ 2(\cos C - \sin C)(\cos C + \sin C) = (\cos C + \sin C) $$

Since $ C $ is an acute angle in a triangle, $ \cos C + \sin C \neq 0 $. Dividing both sides:

$$ 2(\cos C - \sin C) = 1 \Rightarrow \cos C - \sin C = \frac{1}{2} $$

Squaring both sides:

$$ \cos^2 C + \sin^2 C - 2\sin C \cos C = \frac{1}{4} $$

$$ 1 - \sin 2C = \frac{1}{4} \Rightarrow \sin 2C = \frac{3}{4} $$

Also, to find $ \sin C $: substitute $ \cos C = \sin C + \frac{1}{2} $ into $ \sin^2 C + \cos^2 C = 1 $:

$$ \sin^2 C + (\sin C + \frac{1}{2})^2 = 1 $$

$$ 2\sin^2 C + \sin C - \frac{3}{4} = 0 \Rightarrow 8\sin^2 C + 4\sin C - 3 = 0 $$

$$ \sin C = \frac{-4 \pm \sqrt{16 + 96}}{16} = \frac{-4 \pm \sqrt{112}}{16} = \frac{-1 \pm \sqrt{7}}{4} $$

Since $ C $ is a positive angle, $ \sin C = \frac{\sqrt{7}-1}{4} $.

Then $ \cos C = \frac{1}{2} + \frac{\sqrt{7}-1}{4} = \frac{\sqrt{7}+1}{4} $.

Step 3: Calculate Area 'a'

We need $ \sin A $ and $ \sin B $:

$ \sin A = \sin(\frac{\pi}{2} + C) = \cos C = \frac{\sqrt{7}+1}{4} $.

$ \sin B = \cos 2C = 1 - 2\sin^2 C $ or use $ \sin 2C = 3/4 $ earlier? Actually, easier: $ \sin B = \cos 2C = \cos^2 C - \sin^2 C = (\cos C - \sin C)(\cos C + \sin C) = \frac{1}{2}(\cos C + \sin C) $.

Let's use the explicit values:

$ \sin B = \frac{2\sqrt{7}}{4} \times \frac{1}{2} = \frac{\sqrt{7}}{4} $.

Area $ a = 2R^2 \sin A \sin B \sin C = 2(1)^2 \left(\frac{\sqrt{7}+1}{4}\right) \left(\frac{\sqrt{7}}{4}\right) \left(\frac{\sqrt{7}-1}{4}\right) $.

$$ a = 2 \cdot \frac{(\sqrt{7}+1)(\sqrt{7}-1)}{16} \cdot \frac{\sqrt{7}}{4} = 2 \cdot \frac{6}{16} \cdot \frac{\sqrt{7}}{4} = \frac{12\sqrt{7}}{64} = \frac{3\sqrt{7}}{16} $$

Step 4: Calculate $ (64a)^2 $

$$ 64a = 64 \left( \frac{3\sqrt{7}}{16} \right) = 12\sqrt{7} $$

$$ (64a)^2 = (12\sqrt{7})^2 = 144 \times 7 = 1008 $$

Bloom Level

Evaluate

Topic

Trigonometry

Difficulty

4

Ideal Time

180

Sub-topics

Solution of Triangles Sine Rule Trigonometric Identities

PRIMARY SKILL TESTED

Solving geometric problems using trigonometric identities and sine rule

Q.15

Then the inradius of the triangle $ABC$ is

0.25

Solution

Step 1: Formula for Inradius

The inradius $ r $ is given by $ r = \frac{\Delta}{s} $, where $ \Delta $ is the area of the triangle and $ s $ is the semi-perimeter.

From the previous question, we know:

$$ \Delta = a = \frac{3\sqrt{7}}{16} $$

Step 2: Calculate Semi-perimeter 's'

The semi-perimeter $ s = \frac{a_{side} + b_{side} + c_{side}}{2} $.

Using $ a_{side} = 2R \sin A $, etc., with $ R = 1 $:

$$ s = \sin A + \sin B + \sin C $$

Using the values derived in the previous solution:

$ \sin A = \frac{\sqrt{7}+1}{4} $

$ \sin B = \frac{\sqrt{7}}{4} $

$ \sin C = \frac{\sqrt{7}-1}{4} $

$$ s = \frac{\sqrt{7}+1 + \sqrt{7} + \sqrt{7}-1}{4} = \frac{3\sqrt{7}}{4} $$

Step 3: Calculate Inradius 'r'

$$ r = \frac{\Delta}{s} = \frac{\frac{3\sqrt{7}}{16}}{\frac{3\sqrt{7}}{4}} $$

$$ r = \frac{3\sqrt{7}}{16} \times \frac{4}{3\sqrt{7}} = \frac{4}{16} = \frac{1}{4} $$

$$ r = 0.25 $$

Bloom Level

Apply

Topic

Trigonometry

Difficulty

3

Ideal Time

90

Sub-topics

Inradius Area of Triangle

PRIMARY SKILL TESTED

Calculating inradius using area and semi-perimeter relationships

PARAGRAPH "II"

Consider the $6 \times 6$ square in the figure. Let $A_1, A_2, \dots, A_{49}$ be the points of intersections (dots in the picture) in some order. We say that $A_i$ and $A_j$ are friends if they are adjacent along a row or along a column. Assume that each point $A_i$ has an equal chance of being chosen.

Q.16

Let $p_i$ be the probability that a randomly chosen point has $i$ many friends, $i=0,1,2,3,4$. Let $X$ be a random variable such that for $i=0,1,2,3,4$, the probability $P(X=i) = p_i$. Then the value of $7E(X)$ is

24

Solution

Step 1: Understand the Geometry and Random Variable X

The problem considers a $ 6 \times 6 $ square grid. The "points of intersection" form a grid of dots. A $ 6 \times 6 $ square has $ 7 $ dots along each side (counting from index 0 to 6). Total number of points $ N = 7 \times 7 = 49 $.

$ X $ is the number of "friends" (adjacent neighbors) a point has.

Step 2: Classify Points by Number of Neighbors

Corner Points: (4 corners). Each has 2 neighbors.
- Number of points = 4
- $ P(X=2) = \frac{4}{49} $
Edge Points (excluding corners): Points on the boundary but not corners.
- There are 4 sides. Each side has $ 7 - 2 = 5 $ interior edge points.
- Total = $ 4 \times 5 = 20 $.
- Each has 3 neighbors.
- $ P(X=3) = \frac{20}{49} $
Interior Points: Points strictly inside the grid.
- Grid size for interior is $ 5 \times 5 $.
- Total = 25.
- Each has 4 neighbors.
- $ P(X=4) = \frac{25}{49} $

There are no points with 0 or 1 neighbor in a connected grid of this size. $ P(X=0) = P(X=1) = 0 $.

Step 3: Calculate Expectation E(X)

$$ E(X) = \sum x_i P(X=x_i) $$

$$ E(X) = 2 \cdot P(X=2) + 3 \cdot P(X=3) + 4 \cdot P(X=4) $$

$$ E(X) = 2 \cdot \frac{4}{49} + 3 \cdot \frac{20}{49} + 4 \cdot \frac{25}{49} $$

$$ E(X) = \frac{8 + 60 + 100}{49} = \frac{168}{49} $$

Simplifying the fraction (both divisible by 7):

$$ E(X) = \frac{24}{7} $$

Step 4: Find 7E(X)

$$ 7E(X) = 7 \times \frac{24}{7} = 24 $$

Answer: 24

Bloom Level

Apply

Topic

Probability

Difficulty

3

Ideal Time

120

Sub-topics

Random Variables Expected Value Counting on Grids

PRIMARY SKILL TESTED

Calculating expected value based on geometric counting

Q.17

Two distinct points are chosen randomly out of the points $A_1, A_2, \dots, A_{49}$. Let $p$ be the probability that they are friends. Then the value of $7p$ is

0.5

Solution

Step 1: Determine the total number of points and sample space

The problem describes a $ 6 \times 6 $ square grid. The "points of intersection" are the vertices of the grid.

Number of horizontal lines = 7 (indices 0 to 6)
Number of vertical lines = 7 (indices 0 to 6)
Total number of points $ N = 7 \times 7 = 49 $.

We choose 2 distinct points randomly. The total number of ways to choose 2 points from 49 is:

$$ n(S) = \binom{49}{2} = \frac{49 \times 48}{2} = 49 \times 24 = 1176 $$

Step 2: Determine the number of favorable outcomes (Friends)

Points are "friends" if they are adjacent either horizontally or vertically (connected by a grid line segment of length 1).

Horizontal adjacencies: In each of the 7 horizontal lines (rows), there are 7 points, creating $ 7 - 1 = 6 $ adjacent pairs.
Total horizontal pairs = $ 7 \text{ rows} \times 6 \text{ pairs/row} = 42 $.
Vertical adjacencies: In each of the 7 vertical lines (columns), there are 7 points, creating $ 7 - 1 = 6 $ adjacent pairs.
Total vertical pairs = $ 7 \text{ columns} \times 6 \text{ pairs/col} = 42 $.

Total favorable outcomes (number of edges):

$$ n(E) = 42 + 42 = 84 $$

Step 3: Calculate Probability and the Final Value

The probability $ p $ that two randomly chosen points are friends is:

$$ p = \frac{n(E)}{n(S)} = \frac{84}{1176} $$

We need to find the value of $ 7p $:

$$ 7p = 7 \times \frac{84}{49 \times 24} $$

Simplifying the fraction:

$$ 7p = \frac{84}{7 \times 24} $$

$$ 7p = \frac{84}{168} $$

Since $ 168 = 2 \times 84 $:

$$ 7p = \frac{1}{2} = 0.5 $$

Answer: 0.5

Bloom Level

Apply

Topic

Probability

Difficulty

2

Ideal Time

90

Sub-topics

Classical Probability Counting on Grids Combinations

PRIMARY SKILL TESTED

Counting edges in a grid graph relative to total vertex pairs

SECTION 1 (Maximum Marks: 12)

This section contains FOUR (04) questions.
Each question has FOUR options (A), (B), (C) and (D). ONLY ONE of these four options is the correct answer.
Full Marks : +3 If ONLY the correct option is chosen;
Zero Marks : 0 If none of the options is chosen;
Negative Marks : -1 In all other cases.

Q.1

An electric dipole is formed by two charges $+q$ and $-q$ located in $xy$-plane at $(0,2)$ mm and $(0, -2)$ mm, respectively, as shown in the figure. The electric potential at point P $(100,100)$ mm due to the dipole is $V_0$. The charges $+q$ and $-q$ are then moved to the points $(-1,2)$ mm and $(1, -2)$ mm, respectively. What is the value of electric potential at P due to the new dipole? Diagram

(A)

$V_0/4$

(B)

$V_0/2$

(C)

$V_0/\sqrt{2}$

(D)

$3V_0/4$

(B)

Solution

The electric potential due to a dipole at a point $P$ is given by the formula:

$$ V = \frac{k \vec{p} \cdot \vec{r}}{r^3} $$

where $\vec{p}$ is the dipole moment and $\vec{r}$ is the position vector of point $P$.

Case 1 (Initial Dipole):
The charges are at $(0, 2)$ and $(0, -2)$. The dipole moment $\vec{p}$ points from $-q$ to $+q$.
$$ \vec{p} = q[(0, 2) - (0, -2)] = q(0, 4) = 4q\hat{j} $$ The point $P$ is at $(100, 100)$, so $\vec{r} = 100\hat{i} + 100\hat{j}$.
Calculating the dot product:
$$ \vec{p} \cdot \vec{r} = (4q\hat{j}) \cdot (100\hat{i} + 100\hat{j}) = 400q $$ The initial potential is:
$$ V_0 = \frac{k(400q)}{r^3} $$

Case 2 (New Dipole):
The charges are moved to $(-1, 2)$ ($+q$) and $(1, -2)$ ($-q$).
The new dipole moment $\vec{p}'$ is:
$$ \vec{p}' = q[(-1, 2) - (1, -2)] = q(-2, 4) = -2q\hat{i} + 4q\hat{j} $$ The position vector $\vec{r}$ remains $100\hat{i} + 100\hat{j}$.
Calculating the new dot product:
$$ \vec{p}' \cdot \vec{r} = (-2q\hat{i} + 4q\hat{j}) \cdot (100\hat{i} + 100\hat{j}) $$ $$ = (-2q)(100) + (4q)(100) = -200q + 400q = 200q $$ The new potential is:
$$ V_{new} = \frac{k(200q)}{r^3} $$

Conclusion:
Comparing $V_{new}$ and $V_0$:
$$ \frac{V_{new}}{V_0} = \frac{200q}{400q} = \frac{1}{2} $$ $$ V_{new} = \frac{V_0}{2} $$

Thus, the correct option is (B).

Bloom Level

Analyze

Topic

Electrostatics

Difficulty

3 (Medium)

Ideal Time

90s

Sub-topics

Electric Potential Electric Dipole Vector Algebra

PRIMARY SKILL TESTED

Calculating electric potential due to a dipole using vector components.

Option Distractor Reasons

A

May arise from incorrectly squaring a factor of 2 or calculation error in the dot product.

C

Incorrectly assuming the potential scales with $1/\sqrt{2}$ due to angle decomposition errors.

D

Result of guessing or incorrect vector addition of the new dipole components.

Q.2

Young’s modulus of elasticity $Y$ is expressed in terms of three derived quantities, namely, the gravitational constant $G$, Planck’s constant $h$ and the speed of light $c$, as $Y = c^\alpha h^\beta G^\gamma$. Which of the following is the correct option?

(A)

$\alpha = 7, \beta = -1, \gamma = -2$

(B)

$\alpha = -7, \beta = -1, \gamma = -2$

(C)

$\alpha = 7, \beta = -1, \gamma = 2$

(D)

$\alpha = -7, \beta = 1, \gamma = -2$

(A)

Solution

We use dimensional analysis to find the exponents $\alpha, \beta, \gamma$. The given relation is $Y = c^\alpha h^\beta G^\gamma$.

Step 1: Write the dimensional formula for each quantity.

Young's Modulus ($Y$): $[M L^{-1} T^{-2}]$ (Force/Area)
Speed of light ($c$): $[L T^{-1}]$
Planck's constant ($h$): $[M L^2 T^{-1}]$ (Energy $\times$ Time)
Gravitational constant ($G$): $[M^{-1} L^3 T^{-2}]$

Step 2: Equate dimensions on both sides.

$$ [M L^{-1} T^{-2}] = [L T^{-1}]^\alpha [M L^2 T^{-1}]^\beta [M^{-1} L^3 T^{-2}]^\gamma $$ $$ [M^1 L^{-1} T^{-2}] = [M^{\beta - \gamma} L^{\alpha + 2\beta + 3\gamma} T^{-\alpha - \beta - 2\gamma}] $$

Step 3: Solve the system of linear equations.

Comparing powers of M: $\beta - \gamma = 1 \implies \beta = \gamma + 1$ ... (i)

Comparing powers of T: $-\alpha - \beta - 2\gamma = -2 \implies \alpha + \beta + 2\gamma = 2$ ... (ii)

Comparing powers of L: $\alpha + 2\beta + 3\gamma = -1$ ... (iii)

Substitute (i) into (ii):
$\alpha + (\gamma + 1) + 2\gamma = 2 \implies \alpha + 3\gamma = 1 \implies \alpha = 1 - 3\gamma$.

Substitute $\alpha$ and $\beta$ into (iii):
$(1 - 3\gamma) + 2(\gamma + 1) + 3\gamma = -1$
$1 - 3\gamma + 2\gamma + 2 + 3\gamma = -1$
$3 + 2\gamma = -1 \implies 2\gamma = -4 \implies \gamma = -2$.

Now find $\beta$ and $\alpha$:
$\beta = -2 + 1 = -1$
$\alpha = 1 - 3(-2) = 1 + 6 = 7$.

Thus, $\alpha = 7, \beta = -1, \gamma = -2$.

The correct option is (A).

Bloom Level

Apply

Topic

Units and Dimensions

Difficulty

2 (Easy/Medium)

Ideal Time

80s

Sub-topics

Dimensional Analysis Fundamental Quantities

PRIMARY SKILL TESTED

Checking dimensional consistency and solving systems of linear equations.

Option Distractor Reasons

B

Incorrect sign for $\alpha$ (negative instead of positive) usually due to algebra errors.

C

Incorrect sign for $\gamma$ (positive instead of negative).

D

Incorrect sign for $\alpha$ and $\beta$.

Q.3

A particle of mass $m$ is moving in the $xy$-plane such that its velocity at a point $(x, y)$ is given as $\vec{v} = \alpha (y\hat{x} + 2x\hat{y})$, where $\alpha$ is a non-zero constant. What is the force $\vec{F}$ acting on the particle?

(A)

$\vec{F} = 2m\alpha^2(x\hat{x} + y\hat{y})$

(B)

$\vec{F} = m\alpha^2(y\hat{x} + 2x\hat{y})$

(C)

$\vec{F} = 2m\alpha^2(y\hat{x} + x\hat{y})$

(D)

$\vec{F} = m\alpha^2(x\hat{x} + 2y\hat{y})$

(A)

Solution

The velocity of the particle is given by:

$$ \vec{v} = \alpha(y\hat{x} + 2x\hat{y}) $$

Identifying the components of velocity:

$$ v_x = \frac{dx}{dt} = \alpha y $$ $$ v_y = \frac{dy}{dt} = 2\alpha x $$

The acceleration $\vec{a} = \frac{d\vec{v}}{dt}$ is found by differentiating the components with respect to time using the chain rule.

X-component of acceleration:

$$ a_x = \frac{dv_x}{dt} = \frac{d}{dt}(\alpha y) = \alpha \frac{dy}{dt} $$

Substituting $v_y = 2\alpha x$ for $\frac{dy}{dt}$:

$$ a_x = \alpha(2\alpha x) = 2\alpha^2 x $$

Y-component of acceleration:

$$ a_y = \frac{dv_y}{dt} = \frac{d}{dt}(2\alpha x) = 2\alpha \frac{dx}{dt} $$

Substituting $v_x = \alpha y$ for $\frac{dx}{dt}$:

$$ a_y = 2\alpha(\alpha y) = 2\alpha^2 y $$

Force Calculation:

According to Newton's second law, $\vec{F} = m\vec{a}$:

$$ \vec{F} = m(a_x \hat{x} + a_y \hat{y}) = m(2\alpha^2 x \hat{x} + 2\alpha^2 y \hat{y}) $$ $$ \vec{F} = 2m\alpha^2 (x\hat{x} + y\hat{y}) $$

The correct option is (A).

Bloom Level

Apply

Topic

Kinematics

Difficulty

2 (Medium)

Ideal Time

60s

Sub-topics

Motion in 2D Chain Rule Differentiation Newton's Laws

PRIMARY SKILL TESTED

Applying chain rule to find acceleration from a position-dependent velocity field.

Option Distractor Reasons

B

Fails to apply chain rule correctly, likely confusing $v$ with $a$ or missing factor of 2.

C

Incorrectly swaps $x$ and $y$ variables in the final force expression.

D

Error in differentiation coefficients, leading to incorrect pre-factors for the unit vectors.

Q.4

An ideal gas is in thermodynamic equilibrium. The number of degrees of freedom of a molecule of the gas is $n$. The internal energy of one mole of the gas is $U_n$ and the speed of sound in the gas is $v_n$. At a fixed temperature and pressure, which of the following is the correct option?

(A)

$v_3 < v_6$ and $U_3> U_6$

(B)

$v_5 > v_3$ and $U_3 > U_5$

(C)

$v_5 > v_7$ and $U_5 < U_7$

(D)

$v_6 < v_7$ and $U_6 < U_7$

(C)

Solution

We analyze the dependence of internal energy ($U_n$) and speed of sound ($v_n$) on the degrees of freedom ($n$).

1. Internal Energy ($U_n$):
The internal energy of one mole of an ideal gas is given by: $$ U_n = \frac{n}{2}RT $$ From this relation, $U_n$ is directly proportional to $n$. Therefore: $$ \text{If } n_1 < n_2, \text{ then } U_{n_1} < U_{n_2} $$ Comparing $n=5$ and $n=7$: $$ U_5 < U_7 $$

2. Speed of Sound ($v_n$):
The speed of sound in an ideal gas is given by: $$ v_n = \sqrt{\frac{\gamma RT}{M}} $$ where the adiabatic index $\gamma$ is defined as: $$ \gamma = 1 + \frac{2}{n} $$ As the degrees of freedom $n$ increases, the term $\frac{2}{n}$ decreases, which means $\gamma$ decreases. Since $v_n \propto \sqrt{\gamma}$, the speed of sound decreases as $n$ increases. $$ \text{If } n_1 < n_2, \text{ then } v_{n_1}> v_{n_2} $$ Comparing $n=5$ and $n=7$: $$ v_5 > v_7 $$

Conclusion:
Combining the results, we have $v_5 > v_7$ and $U_5 < U_7$. This matches option (C).

Bloom Level

Analyze

Topic

Thermodynamics

Difficulty

2 (Easy/Medium)

Ideal Time

60s

Sub-topics

Kinetic Theory of Gases Speed of Sound Internal Energy

PRIMARY SKILL TESTED

Conceptual understanding of how degrees of freedom affect thermodynamic properties.

Option Distractor Reasons

A

Incorrectly assumes speed of sound increases with degrees of freedom ($n$).

B

Incorrectly assumes internal energy decreases as degrees of freedom ($n$) increases.

D

Incorrect comparison of speeds; $v_6$ should be greater than $v_7$ because $\gamma_6 > \gamma_7$.

SECTION 2 (Maximum Marks: 12)

This section contains THREE (03) questions.
Each question has FOUR options (A), (B), (C) and (D). ONE OR MORE THAN ONE of these four option(s) is (are) correct answer(s).
Full Marks : +4 ONLY if (all) the correct option(s) is(are) chosen;
Partial Marks : +3 If all four options are correct but ONLY three options are chosen;
Partial Marks : +2 If three or more options are correct but ONLY two options are chosen, both of which are correct;
Partial Marks : +1 If two or more options are correct but ONLY one option is chosen and it is a correct option;
Zero Marks : 0 If unanswered;
Negative Marks : -2 In all other cases.

Q.5

A monochromatic light wave is incident normally on a glass slab of thickness $d$, as shown in the figure. The refractive index of the slab increases linearly from $n_1$ to $n_2$ over the height $h$. Which of the following statement(s) is(are) true about the light wave emerging out of the slab? Diagram

(A)

It will deflect up by an angle $\tan^{-1}\left[\frac{(n_2^2 - n_1^2)d}{2h}\right]$.

(B)

It will deflect up by an angle $\tan^{-1}\left[\frac{(n_2 - n_1)d}{h}\right]$.

(C)

It will not deflect.

(D)

The deflection angle depends only on $(n_2 - n_1)$ and not on the individual values of $n_1$ and $n_2$.

(B), (D)

Solution

We analyze the deflection by considering the optical path difference traveled by the top and bottom parts of the wavefront.

Step 1: Calculate time taken to cross the slab.
The refractive index varies from $n_1$ at the bottom to $n_2$ at the top. The speed of light in a medium is $v = c/n$. Time taken for the top ray (refractive index $n_2$) to travel distance $d$: $$ t_{top} = \frac{d}{c/n_2} = \frac{n_2 d}{c} $$ Time taken for the bottom ray (refractive index $n_1$) to travel distance $d$: $$ t_{bot} = \frac{d}{c/n_1} = \frac{n_1 d}{c} $$

Step 2: Determine path difference in air.
Since $n_2 > n_1$, $t_{top} > t_{bot}$. The top part lags behind. Consider the wavefront emerging from the slab. In the time difference $\Delta t = t_{top} - t_{bot}$, the bottom ray travels an extra distance $x$ in air (where $n \approx 1$, speed $= c$) to "wait" for the top ray to emerge. $$ x = c \cdot \Delta t = c \left( \frac{n_2 d}{c} - \frac{n_1 d}{c} \right) = d(n_2 - n_1) $$

Step 3: Calculate the deflection angle $\theta$.
The emerging wavefront is tilted. Constructing a triangle with the wavefront height $h$ and the path difference $x$: $$ \tan \theta = \frac{x}{h} $$ Substituting $x = d(n_2 - n_1)$: $$ \tan \theta = \frac{d(n_2 - n_1)}{h} $$ $$ \theta = \tan^{-1} \left[ \frac{(n_2 - n_1)d}{h} \right] $$ This matches Option (B). Additionally, the formula shows the angle depends only on the difference $(n_2 - n_1)$, making Option (D) correct as well.

Bloom Level

Apply

Topic

Optics

Difficulty

3 (Medium)

Ideal Time

90s

Sub-topics

Wave Optics Optical Path Length

PRIMARY SKILL TESTED

Calculating wavefront tilt due to varying optical path lengths.

Option Distractor Reasons

A

Incorrect formula derivation, likely from misapplying average refractive index concepts.

C

Incorrectly assumes no deflection occurs for normal incidence, ignoring the gradient in refractive index.

Q.6

An annular disk of mass $M$, inner radius $a$ and outer radius $b$ is placed on a horizontal surface with coefficient of friction $\mu$, as shown in the figure. At some time, an impulse $\mathcal{J}_0 \hat{x}$ is applied at a height $h$ above the center of the disk. If $h = h_m$ then the disk rolls without slipping along the $x$-axis. Which of the following statement(s) is(are) correct? Diagram

(A)

For $\mu \neq 0$ and $a \to 0$, $h_m = b/2$.

(B)

For $\mu \neq 0$ and $a \to b$, $h_m = b$.

(C)

For $h = h_m$, the initial angular velocity does not depend on the inner radius $a$.

(D)

For $\mu = 0$ and $h = 0$, the wheel always slides without rolling.

(A), (B), (C), (D)

Solution

We analyze the motion using impulse-momentum theorems for translation and rotation.

Step 1: Equations of Motion
Linear Impulse ($J_0$) provides linear momentum: $$ J_0 = M v_{cm} \implies v_{cm} = \frac{J_0}{M} $$ Angular Impulse about the center of mass (CM) provides angular momentum: $$ J_0 \cdot h = I_{cm} \omega \implies \omega = \frac{J_0 h}{I_{cm}} $$

Step 2: Condition for Rolling without Slipping
For immediate rolling without slipping, the velocity of the contact point must be zero. $$ v_{contact} = v_{cm} - b\omega = 0 \implies v_{cm} = b\omega $$ Substituting the expressions for $v_{cm}$ and $\omega$: $$ \frac{J_0}{M} = b \left( \frac{J_0 h_m}{I_{cm}} \right) $$ $$ \frac{1}{M} = \frac{b h_m}{I_{cm}} \implies h_m = \frac{I_{cm}}{Mb} $$

Step 3: Analyze for Annular Disk
The moment of inertia for an annular disk is $I_{cm} = \frac{M}{2}(a^2 + b^2)$. Substituting this into the height equation: $$ h_m = \frac{\frac{M}{2}(a^2 + b^2)}{Mb} = \frac{a^2 + b^2}{2b} $$

Step 4: Evaluate Options
(A) If $a \to 0$ (solid disk): $h_m = \frac{0 + b^2}{2b} = \frac{b}{2}$. (Correct)
(B) If $a \to b$ (ring): $h_m = \frac{b^2 + b^2}{2b} = b$. (Correct)
(C) At $h=h_m$, angular velocity $\omega = \frac{v_{cm}}{b}$. Since $v_{cm} = J_0/M$, $\omega = \frac{J_0}{Mb}$. This expression does not depend on the inner radius $a$. (Correct)
(D) If $\mu=0$ (frictionless) and $h=0$: Impulse passes through CM, so torque $\tau=0 \implies \omega=0$. However, $F \neq 0 \implies v_{cm} \neq 0$. The wheel translates without rotating (pure sliding). (Correct)

Thus, all options (A), (B), (C), and (D) are correct.

Bloom Level

Evaluate

Topic

Rotational Mechanics

Difficulty

3 (Medium)

Ideal Time

120s

Sub-topics

Impulse-Momentum Theorem Rolling Motion Moment of Inertia

PRIMARY SKILL TESTED

Applying conservation laws and conditions for pure rolling to a rigid body system.

Q.7

The electric field associated with an electromagnetic wave propagating in a dielectric medium is given by $\vec{E} = 30(2\hat{x} + \hat{y})\sin \left[2\pi \left(5 \times 10^{14} t - \frac{10^7}{3} z\right)\right]$ V m$^{-1}$. Which of the following option(s) is(are) correct?
[Given: The speed of light in vacuum, $c = 3 \times 10^8$ m s$^{-1}$]

(A)

$B_x = -2 \times 10^{-7} \sin \left[2\pi \left(5 \times 10^{14} t - \frac{10^7}{3} z\right)\right]$ Wb m$^{-2}$.

(B)

$B_y = 2 \times 10^{-7} \sin \left[2\pi \left(5 \times 10^{14} t - \frac{10^7}{3} z\right)\right]$ Wb m$^{-2}$.

(C)

The wave is polarized in the $xy$-plane with polarization angle $30^\circ$ with respect to the $x$-axis.

(D)

The refractive index of the medium is 2.

(A), (D)

Solution

Step 1: Determine the wave properties from the Electric Field equation.
The given electric field is $\vec{E} = 30(2\hat{x} + \hat{y}) \sin\left[ 2\pi(5 \times 10^{14} t - \frac{10^7}{3} z) \right]$.
Comparing this with the standard wave equation $\vec{E} = \vec{E}_0 \sin(\omega t - kz)$, we identify:

Angular frequency $\omega = 2\pi \times 5 \times 10^{14}$ rad/s
Wave number $k = 2\pi \times \frac{10^7}{3}$ m⁻¹

Step 2: Calculate the Refractive Index (Option D).
The speed of the wave in the medium is $v = \frac{\omega}{k}$. $$ v = \frac{2\pi \times 5 \times 10^{14}}{2\pi \times \frac{10^7}{3}} = 15 \times 10^7 = 1.5 \times 10^8 \text{ m/s} $$ The refractive index $n$ is the ratio of the speed of light in vacuum to the speed in the medium: $$ n = \frac{c}{v} = \frac{3 \times 10^8}{1.5 \times 10^8} = 2 $$ Thus, Option (D) is correct.

Step 3: Analyze the Polarization (Option C).
The direction of polarization is the direction of the electric field vector $\vec{E}_0 = 2\hat{x} + \hat{y}$. The angle $\theta$ this vector makes with the x-axis is given by: $$ \tan \theta = \frac{E_y}{E_x} = \frac{1}{2} \implies \theta = \tan^{-1}(0.5) $$ Since $\tan^{-1}(0.5) \neq 30^\circ$, Option (C) is incorrect.

Step 4: Determine the Magnetic Field $\vec{B}$.
The magnitude of the magnetic field amplitude is $B_0 = \frac{E_0}{v}$. Magnitude of $\vec{E}_0$ is $30\sqrt{2^2 + 1^2} = 30\sqrt{5}$ V/m. $$ B_0 = \frac{30\sqrt{5}}{1.5 \times 10^8} = 20\sqrt{5} \times 10^{-8} \text{ T} $$ The direction of propagation is $\hat{k} = \hat{z}$. The direction of $\vec{E}$ is $\hat{e} = \frac{2\hat{x} + \hat{y}}{\sqrt{5}}$. The direction of $\vec{B}$ is $\hat{b} = \hat{k} \times \hat{e} = \hat{z} \times \frac{2\hat{x} + \hat{y}}{\sqrt{5}} = \frac{1}{\sqrt{5}}(2(\hat{z}\times\hat{x}) + (\hat{z}\times\hat{y})) = \frac{2\hat{y} - \hat{x}}{\sqrt{5}}$. So, the vector $\vec{B} = B_0 \hat{b} \sin(\dots) = (20\sqrt{5} \times 10^{-8}) \left( \frac{-\hat{x} + 2\hat{y}}{\sqrt{5}} \right) \sin(\dots)$. $$ \vec{B} = 20 \times 10^{-8} (-\hat{x} + 2\hat{y}) \sin(\dots) $$ $$ \vec{B} = (-2 \times 10^{-7} \hat{x} + 4 \times 10^{-7} \hat{y}) \sin(\dots) $$ Comparing components: $B_x = -2 \times 10^{-7} \sin(\dots)$ (Matches Option A) $B_y = 4 \times 10^{-7} \sin(\dots)$ (Does not match Option B, which has $2 \times 10^{-7}$) Thus, Option (A) is correct and Option (B) is incorrect.

Bloom Level

Analyze

Topic

Electromagnetic Waves

Difficulty

3 (Medium)

Ideal Time

100s

Sub-topics

Wave Equation Poynting Vector Direction Refractive Index

PRIMARY SKILL TESTED

Relating electric and magnetic field vectors in an EM wave and calculating wave speed in dielectric media.

Option Distractor Reasons

B

Incorrect amplitude calculation, likely missing the factor of 2 from the cross product or component decomposition.

C

Assumes a standard angle like 30° instead of calculating $\tan^{-1}(1/2)$.

SECTION 3 (Maximum Marks: 24)

This section contains SIX (06) questions.
The answer to each question is a NON-NEGATIVE INTEGER.
Full Marks : +4 If ONLY the correct integer is entered;
Zero Marks : 0 In all other cases.

Q.8

A thin circular coin of mass 5 gm and radius 4/3 cm is initially in a horizontal $xy$-plane. The coin is tossed vertically up (+z direction) by applying an impulse of $\sqrt{\frac{\pi}{2}} \times 10^{-2}$ N-s at a distance 2/3 cm from its center. The coin spins about its diameter and moves along the +z direction. By the time the coin reaches back to its initial position, it completes $n$ rotations. The value of $n$ is ____.
[Given: The acceleration due to gravity $g = 10$ m s$^{-2}$] Diagram

30

Solution

This problem involves linear motion under gravity and rotational motion imparted by an impulsive force.

Step 1: Calculate Linear Velocity ($v_{cm}$) and Angular Velocity ($\omega$).
The impulse $J$ acts at a distance $h = 2/3$ cm from the center. Linear Impulse-Momentum Theorem: $$ J = mv_{cm} \implies v_{cm} = \frac{J}{m} $$ Angular Impulse-Momentum Theorem: $$ J \cdot h = I \omega $$ The coin rotates about its diameter, so the moment of inertia $I = \frac{mR^2}{4}$. $$ \omega = \frac{Jh}{I} = \frac{Jh}{mR^2/4} = \frac{4Jh}{mR^2} $$ Given $h = 2/3$ cm and radius $R = 4/3$ cm, we see that $h = R/2$. $$ \omega = \frac{4J(R/2)}{mR^2} = \frac{2J}{mR} $$

Step 2: Calculate Time of Flight ($T$).
The coin is tossed vertically. The time to return to the initial position is: $$ T = \frac{2v_{cm}}{g} = \frac{2J}{mg} $$

Step 3: Calculate Total Angle of Rotation ($\theta$).
$$ \theta = \omega T = \left( \frac{2J}{mR} \right) \left( \frac{2J}{mg} \right) = \frac{4J^2}{m^2 R g} $$

Step 4: Substitute Values.
$J = \sqrt{\frac{\pi}{2}} \times 10^{-2}$ Ns $\implies J^2 = \frac{\pi}{2} \times 10^{-4}$
$m = 5 \text{ gm} = 5 \times 10^{-3}$ kg
$R = \frac{4}{3} \text{ cm} = \frac{4}{3} \times 10^{-2}$ m
$g = 10$ m/s²
$$ \theta = \frac{4 \left( \frac{\pi}{2} \times 10^{-4} \right)}{(5 \times 10^{-3})^2 \left( \frac{4}{3} \times 10^{-2} \right) (10)} $$ $$ \theta = \frac{2\pi \times 10^{-4}}{25 \times 10^{-6} \times \frac{40}{3} \times 10^{-2}} $$ $$ \theta = \frac{2\pi \times 10^{-4}}{\frac{1000}{3} \times 10^{-8}} = \frac{6\pi \times 10^{-4}}{1000 \times 10^{-8}} = \frac{6\pi \times 10^{-4}}{10^{-5}} = 60\pi $$

Step 5: Determine Number of Rotations ($n$).
$$ n = \frac{\theta}{2\pi} = \frac{60\pi}{2\pi} = 30 $$ The value of $n$ is 30.

Bloom Level

Evaluate

Topic

Mechanics

Difficulty

4 (Hard)

Ideal Time

150s

Sub-topics

Impulse Angular Momentum Kinematics

PRIMARY SKILL TESTED

Combining linear and rotational dynamics with kinematics to solve for total rotation.

Q.9

A rectangular conducting loop of length 4 cm and width 2 cm is in the $xy$-plane, as shown in the figure. It is being moved away from a thin and long conducting wire along the direction $\frac{\sqrt{3}}{2}\hat{x} + \frac{1}{2}\hat{y}$ with a constant speed v. The wire is carrying a steady current $I = 10$ A in the positive $x$-direction. A current of 10 $\mu$A flows through the loop when it is at a distance $d = 4$ cm from the wire. If the resistance of the loop is 0.1 $\Omega$, then the value of v is _______ m s$^{-1}$.
[Given: The permeability of free space $\mu_0 = 4\pi \times 10^{-7}$ N A$^{-2}$] Diagram

4

Solution

We calculate the induced EMF using the rate of change of magnetic flux.

Step 1: Calculate the Magnetic Flux ($\Phi$) through the loop.
Consider a small strip of width $dy$ parallel to the long wire at a distance $y$. The magnetic field at distance $y$ is $B = \frac{\mu_0 I}{2\pi y}$. The area of the strip is $dA = w dy$, where $w = 2 \text{ cm}$ is the width of the loop parallel to the wire. The total flux through the loop (which extends from $y=d$ to $y=d+h$, where $h=4 \text{ cm}$) is: $$ \Phi = \int_d^{d+h} \frac{\mu_0 I}{2\pi y} w dy = \frac{\mu_0 I w}{2\pi} \ln\left( \frac{d+h}{d} \right) $$

Step 2: Calculate Induced EMF ($\varepsilon$).
The loop moves away such that the distance $d$ changes with time. The velocity component perpendicular to the wire ($v_y$) is responsible for the change in flux. The velocity vector is along $\frac{\sqrt{3}}{2}\hat{x} + \frac{1}{2}\hat{y}$, so $v_y = v \sin 30^\circ = v/2$. Using Faraday's Law ($\varepsilon = \left| \frac{d\Phi}{dt} \right|$): $$ \frac{d\Phi}{dt} = \frac{d\Phi}{dd} \frac{dd}{dt} = \frac{\mu_0 I w}{2\pi} \left[ \frac{d}{d+h} \cdot \frac{-(d+h)+d}{d^2} \right] v_y $$ Actually, differentiating $\ln(1 + h/d)$ with respect to $d$: $$ \frac{d}{dd} \ln\left( \frac{d+h}{d} \right) = \frac{1}{\frac{d+h}{d}} \cdot \frac{d(1) - (d+h)(1)}{d^2} = \frac{d}{d+h} \cdot \frac{-h}{d^2} = \frac{-h}{d(d+h)} $$ So, magnitude of EMF: $$ \varepsilon = \frac{\mu_0 I w h}{2\pi d(d+h)} v_y $$

Step 3: Solve for velocity ($v$).
Given: $\varepsilon = iR = (10 \mu\text{A})(0.1 \Omega) = 10^{-6} \text{ V}$. Substitutions (in SI units): $I = 10 \text{ A}$, $w = 0.02 \text{ m}$, $h = 0.04 \text{ m}$, $d = 0.04 \text{ m}$, $v_y = v/2$. $$ 10^{-6} = \frac{(4\pi \times 10^{-7})(10)(0.02)(0.04)}{2\pi (0.04)(0.08)} \left( \frac{v}{2} \right) $$ Simplifying: $$ 10^{-6} = \frac{2 \times 10^{-7} \times 10 \times 0.02 \times 0.04}{0.0032} \times \frac{v}{2} $$ $$ 10^{-6} = \frac{1.6 \times 10^{-9}}{0.0032} \times \frac{v}{2} $$ $$ 10^{-6} = (5 \times 10^{-7}) \frac{v}{2} $$ $$ 2 \times 10^{-6} = 5 \times 10^{-7} v $$ $$ v = \frac{20 \times 10^{-7}}{5 \times 10^{-7}} = 4 \text{ m/s} $$

Bloom Level

Apply

Topic

Electromagnetism

Difficulty

3 (Medium)

Ideal Time

90s

Sub-topics

Motional EMF Magnetic Flux Faraday's Law

PRIMARY SKILL TESTED

Calculating induced EMF in a moving loop due to a non-uniform magnetic field.

Q.10

A string of length 1 m and mass $2 \times 10^{-5}$ kg is under tension $T$. When the string vibrates, two successive harmonics are found to occur at frequencies 750 Hz and 1000 Hz. The value of tension $T$ is _____ Newton.

5

Solution

The frequency of harmonics in a string fixed at both ends is given by $f_n = \frac{nv}{2L}$, where $n$ is the harmonic number, $v$ is the wave speed, and $L$ is the length.

Given two successive harmonics have frequencies $f_n = 750 \text{ Hz}$ and $f_{n+1} = 1000 \text{ Hz}$. The difference between consecutive harmonic frequencies corresponds to the fundamental frequency ($f_1$): $$ f_1 = f_{n+1} - f_n = 1000 - 750 = 250 \text{ Hz} $$

The fundamental frequency is related to tension $T$ and linear mass density $\mu$ by: $$ f_1 = \frac{1}{2L}\sqrt{\frac{T}{\mu}} $$ Rearranging to solve for tension $T$: $$ T = \mu (2L f_1)^2 $$

Given:

Length $L = 1 \text{ m}$
Mass $m = 2 \times 10^{-5} \text{ kg} \implies \mu = \frac{m}{L} = 2 \times 10^{-5} \text{ kg/m}$
$f_1 = 250 \text{ Hz}$

Substituting values: $$ T = (2 \times 10^{-5}) \times (2 \times 1 \times 250)^2 $$ $$ T = (2 \times 10^{-5}) \times (500)^2 $$ $$ T = 2 \times 10^{-5} \times 250000 = 5 \text{ N} $$ The tension $T$ is 5 Newton.

Bloom Level

Apply

Topic

Waves

Difficulty

2 (Easy/Medium)

Ideal Time

60s

Sub-topics

Standing Waves Vibration of Strings

PRIMARY SKILL TESTED

Calculating tension from fundamental frequency and linear mass density.

Q.11

An incompressible liquid is kept in a container having a weightless piston with a hole. A capillary tube of inner radius 0.1 mm is dipped vertically into the liquid through the airtight piston hole, as shown in the figure. The air in the container is isothermally compressed from its original volume $V_0$ to $\frac{100}{101}V_0$ with the movable piston. Considering air as an ideal gas, the height ($h$) of the liquid column in the capillary above the liquid level in cm is_______.
[Given: Surface tension of the liquid is 0.075 N m$^{-1}$, atmospheric pressure is $10^5$ N m$^{-2}$, acceleration due to gravity ($g$) is 10 m s$^{-2}$, density of the liquid is $10^3$ kg m$^{-3}$ and contact angle of capillary surface with the liquid is zero] Diagram

25

Solution

We need to balance the pressure inside the liquid column by considering the compressed air pressure and capillary forces.

Step 1: Calculate the pressure of the compressed air ($P_{in}$).
Since the air is compressed isothermally from $V_0$ to $\frac{100}{101}V_0$, using Boyle's Law ($P_1 V_1 = P_2 V_2$): $$ P_0 V_0 = P_{in} \left( \frac{100}{101} V_0 \right) \implies P_{in} = \frac{101}{100} P_0 $$

Step 2: Analyze pressure at the meniscus.
The capillary is open to the atmosphere, so the pressure just above the meniscus is $P_0$. For a wetting liquid (contact angle 0), the meniscus is concave up. The pressure on the concave side (air) is higher than the convex side (liquid) by $\frac{2T}{r}$. $$ P_{above} - P_{below} = \frac{2T}{r} \implies P_0 - P_{liquid\_top} = \frac{2T}{r} $$ $$ P_{liquid\_top} = P_0 - \frac{2T}{r} $$

Step 3: Relate pressures via hydrostatic equation.
The pressure at the flat liquid surface outside the tube is equal to the compressed air pressure $P_{in}$. The pressure inside the tube at the same horizontal level (at depth $h$ below the meniscus) must also be $P_{in}$. $$ P_{in} = P_{liquid\_top} + \rho g h $$ Substituting the expressions derived: $$ \frac{101}{100} P_0 = \left( P_0 - \frac{2T}{r} \right) + \rho g h $$

Step 4: Solve for $h$.
$$ \rho g h = \frac{101}{100} P_0 - P_0 + \frac{2T}{r} $$ $$ \rho g h = \frac{1}{100} P_0 + \frac{2T}{r} $$ Substituting given values ($P_0 = 10^5, T = 0.075, r = 10^{-4}, \rho = 10^3, g = 10$): $$ 10^4 h = \frac{10^5}{100} + \frac{2(0.075)}{10^{-4}} $$ $$ 10^4 h = 1000 + 1500 = 2500 $$ $$ h = \frac{2500}{10000} = 0.25 \text{ m} $$ In cm, $h = 25 \text{ cm}$.

Bloom Level

Analyze

Topic

Fluid Mechanics

Difficulty

4 (Hard)

Ideal Time

150s

Sub-topics

Capillary Action Hydrostatic Pressure Ideal Gas Law

PRIMARY SKILL TESTED

Combining thermodynamics (isothermal process) with fluid statics (capillary pressure difference).

Q.12

In a radioactive decay process, the activity is defined as $A = -\frac{dN}{dt}$, where $N(t)$ is the number of radioactive nuclei at time $t$. Two radioactive sources, $S_1$ and $S_2$ have same activity at time $t=0$. At a later time, the activities of $S_1$ and $S_2$ are $A_1$ and $A_2$, respectively. When $S_1$ and $S_2$ have just completed their 3rd and 7th half-lives, respectively, the ratio $A_1/A_2$ is __________.

16

Solution

The activity $A$ of a radioactive source is given by the formula:

$$ A = A_0 \left( \frac{1}{2} \right)^n $$

where $A_0$ is the initial activity and $n$ is the number of half-lives elapsed.

For source $S_1$, $n = 3$: $$ A_1 = A_0 \left( \frac{1}{2} \right)^3 $$

For source $S_2$, $n = 7$: $$ A_2 = A_0 \left( \frac{1}{2} \right)^7 $$

To find the ratio $A_1/A_2$: $$ \frac{A_1}{A_2} = \frac{A_0 (1/2)^3}{A_0 (1/2)^7} $$ $$ \frac{A_1}{A_2} = \left( \frac{1}{2} \right)^{3-7} = \left( \frac{1}{2} \right)^{-4} $$ $$ \frac{A_1}{A_2} = 2^4 = 16 $$ The ratio is 16.

Bloom Level

Apply

Topic

Modern Physics

Difficulty

1 (Easy)

Ideal Time

45s

Sub-topics

Radioactivity Half-Life

PRIMARY SKILL TESTED

Calculating radioactive activity based on the number of half-lives.

Q.13

One mole of an ideal gas undergoes two different cyclic processes I and II, as shown in the $P-V$ diagrams below. In cycle I, processes $a, b, c$ and $d$ are isobaric, isothermal, isobaric and isochoric, respectively. In cycle II, processes $a', b', c'$ and $d'$ are isothermal, isochoric, isobaric and isochoric, respectively. The total work done during cycle I is $W_I$ and that during cycle II is $W_{II}$. The ratio $W_I/W_{II}$ is _______. Diagram

2

Solution

We calculate the total work done for each cycle by summing the work done in individual processes. Work done is the area under the $P-V$ curve ($W = \int P dV$).

Cycle I:
1. Process a (Isobaric expansion): From $(V_0, 4P_0)$ to $(2V_0, 4P_0)$. $$ W_a = P \Delta V = 4P_0(2V_0 - V_0) = 4P_0V_0 $$ 2. Process b (Isothermal expansion): From $(2V_0, 4P_0)$ to $(4V_0, 2P_0)$. $$ W_b = nRT \ln\left(\frac{V_f}{V_i}\right) = P_i V_i \ln\left(\frac{V_f}{V_i}\right) = (4P_0)(2V_0) \ln\left(\frac{4V_0}{2V_0}\right) = 8P_0V_0 \ln 2 $$ 3. Process c (Isobaric compression): From $(4V_0, 2P_0)$ to $(V_0, 2P_0)$. $$ W_c = P \Delta V = 2P_0(V_0 - 4V_0) = -6P_0V_0 $$ 4. Process d (Isochoric): Volume constant at $V_0$. $$ W_d = 0 $$ Total Work $W_I$: $$ W_I = 4P_0V_0 + 8P_0V_0 \ln 2 - 6P_0V_0 = 8P_0V_0 \ln 2 - 2P_0V_0 $$ $$ W_I = 2P_0V_0(4 \ln 2 - 1) $$

Cycle II:
1. Process a' (Isothermal expansion): From $(V_0, 4P_0)$ to $(2V_0, 2P_0)$. $$ W_{a'} = (4P_0)(V_0) \ln\left(\frac{2V_0}{V_0}\right) = 4P_0V_0 \ln 2 $$ 2. Process b' (Isochoric): Volume constant at $2V_0$. $$ W_{b'} = 0 $$ 3. Process c' (Isobaric compression): From $(2V_0, P_0)$ to $(V_0, P_0)$. $$ W_{c'} = P_0(V_0 - 2V_0) = -P_0V_0 $$ 4. Process d' (Isochoric): Volume constant at $V_0$. $$ W_{d'} = 0 $$ Total Work $W_{II}$: $$ W_{II} = 4P_0V_0 \ln 2 - P_0V_0 = P_0V_0(4 \ln 2 - 1) $$

Ratio: $$ \frac{W_I}{W_{II}} = \frac{2P_0V_0(4 \ln 2 - 1)}{P_0V_0(4 \ln 2 - 1)} = 2 $$

Bloom Level

Analyze

Topic

Thermodynamics

Difficulty

2 (Medium)

Ideal Time

90s

Sub-topics

Work Done in Cyclic Process Isothermal Process PV Diagram Analysis

PRIMARY SKILL TESTED

Calculating work done for various thermodynamic processes using PV graphs.

SECTION 4 (Maximum Marks: 12)

This section contains TWO (02) paragraphs.
Based on each paragraph, there are TWO (02) questions.
The answer to each question is a NUMERICAL VALUE.
If the numerical value has more than two decimal places, truncate/round-off the value to TWO decimal places.
Full Marks : +3 If ONLY the correct numerical value is entered;
Zero Marks : 0 In all other cases.

PARAGRAPH I

$S_1$ and $S_2$ are two identical sound sources of frequency 656 Hz. The source $S_1$ is located at $O$ and $S_2$ moves anti-clockwise with a uniform speed $4\sqrt{2}$ m s$^{-1}$ on a circular path around $O$, as shown in the figure. There are three points $P, Q$ and $R$ on this path such that $P$ and $R$ are diametrically opposite while $Q$ is equidistant from them. A sound detector is placed at point $P$. The source $S_1$ can move along direction $OP$.
[Given: The speed of sound in air is 324 m s$^{-1}$]

Q.14

When only $S_2$ is emitting sound and it is at $Q$, the frequency of sound measured by the detector in Hz is _________.

648

Solution

Given:
Source frequency $f_0 = 656 \text{ Hz}$.
Speed of sound $v = 324 \text{ m/s}$.
Source speed $v_s = 4\sqrt{2} \text{ m/s}$.

Analysis:
The detector is at P (let's assume position at angle $270^\circ$ or $-\pi/2$). The source $S_2$ is at Q, which is equidistant from P and R (where R is diametrically opposite to P). Thus, Q corresponds to an angle of $0^\circ$ or $180^\circ$. From the diagram, P is at the bottom and Q is to the right ($0^\circ$). The angle subtended by the arc PQ at the center O is $90^\circ$.
The triangle $\Delta OPQ$ is an isosceles right-angled triangle. Therefore, the angle $\angle OQP = 45^\circ$.

The velocity of source $S_2$ is tangential to the circular path. At Q, the velocity vector $\vec{v}_s$ is perpendicular to the radius OQ. The line of sight QP makes an angle of $45^\circ$ with the radius OQ. Therefore, the angle between the velocity vector $\vec{v}_s$ and the line of sight QP is $90^\circ - 45^\circ = 45^\circ$.

Since $S_2$ moves anti-clockwise, at Q (rightmost point), its velocity is directed upwards. The detector P is at the bottom. The source is moving away from the detector. The component of source velocity along the line of sight QP is: $$ v_{s,\parallel} = v_s \cos 45^\circ = (4\sqrt{2}) \cdot \frac{1}{\sqrt{2}} = 4 \text{ m/s} $$

Calculation:
Using the Doppler effect formula for a source moving away: $$ f = f_0 \left( \frac{v}{v + v_{s,\parallel}} \right) $$ $$ f = 656 \left( \frac{324}{324 + 4} \right) = 656 \left( \frac{324}{328} \right) $$ $$ f = 656 \left( \frac{81}{82} \right) $$ Since $656 / 82 = 8$: $$ f = 8 \times 81 = 648 \text{ Hz} $$

Bloom Level

Apply

Topic

Waves

Difficulty

3 (Medium)

Ideal Time

60s

Sub-topics

Doppler Effect Vector Components

PRIMARY SKILL TESTED

Applying the Doppler effect formula for a source moving at an angle to the line of sight.

Q.15

Consider both sources emitting sound. When $S_2$ is at $R$ and $S_1$ approaches the detector with a speed 4 m s$^{-1}$, the beat frequency measured by the detector is _______ Hz.

8.2

Solution

We need to find the beat frequency, which is the difference between the apparent frequencies of the two sources observed at P.

Source 1 ($S_1$):
$S_1$ is at the center but moving towards the detector P with speed $v_{s1} = 4 \text{ m/s}$.
Since the source is approaching the observer: $$ f_1 = f_0 \left( \frac{v}{v - v_{s1}} \right) $$ $$ f_1 = 656 \left( \frac{324}{324 - 4} \right) = 656 \left( \frac{324}{320} \right) $$ $$ f_1 = 656 \times 1.0125 = 664.2 \text{ Hz} $$

Source 2 ($S_2$):
$S_2$ is at R (diametrically opposite to P). The velocity of $S_2$ is tangential to the circle. Since RP is the diameter, the velocity vector at R is perpendicular to the line of sight RP.
The component of velocity along the line of sight is $v_{s2} \cos 90^\circ = 0$. Therefore, there is no Doppler shift for $S_2$. $$ f_2 = f_0 = 656 \text{ Hz} $$

Beat Frequency:
$$ f_{beat} = |f_1 - f_2| = |664.2 - 656| = 8.2 \text{ Hz} $$

Bloom Level

Evaluate

Topic

Waves

Difficulty

3 (Medium)

Ideal Time

75s

Sub-topics

Beats Doppler Effect

PRIMARY SKILL TESTED

Calculating beat frequency by determining Doppler shifts for multiple moving sources.

PARAGRAPH II

A cylindrical furnace has height ($H$) and diameter ($D$) both 1 m. It is maintained at temperature 360 K. The air gets heated inside the furnace at constant pressure $P_a$ and its temperature becomes $T = 360$ K. The hot air with density $\rho$ rises up a vertical chimney of diameter $d = 0.1$ m and height $h = 9$ m above the furnace and exits the chimney (see the figure). As a result, atmospheric air of density $\rho_a = 1.2$ kg m$^{-3}$, pressure $P_a$ and temperature $T_a = 300$ K enters the furnace. Assume air as an ideal gas, neglect the variations in $\rho$ and $T$ inside the chimney and the furnace. Also ignore the viscous effects.
[Given: The acceleration due to gravity $g = 10$ m s$^{-2}$ and $\pi = 3.14$]

Q.16

Considering the air flow to be streamline, the steady mass flow rate of air exiting the chimney is _______ gm s$^{-1}$.

49.61

Solution

Step 1: Calculate the density of the hot air.
The pressure inside the furnace and chimney is approximately atmospheric (open system). Using the ideal gas law for constant pressure ($P \propto \rho T$ is constant): $$ \rho T = \rho_a T_a $$ $$ \rho = \rho_a \left( \frac{T_a}{T} \right) = 1.2 \left( \frac{300}{360} \right) = 1.2 \left( \frac{5}{6} \right) = 1.0 \text{ kg/m}^3 $$

Step 2: Apply Bernoulli's Equation.
Consider a streamline entering from the bottom (point 1) and exiting at the top (point 2). Let $L = H + h = 1 + 9 = 10 \text{ m}$.

At inlet (1): $v_1 \approx 0$, $P_1 = P_a$, $z_1 = 0$.
At exit (2): $v_2 = v$, $P_2 = P_{atm}(L) = P_a - \rho_a g L$, $z_2 = L$.

Using Bernoulli's equation: $$ P_1 + \frac{1}{2}\rho v_1^2 + \rho g z_1 = P_2 + \frac{1}{2}\rho v_2^2 + \rho g z_2 $$ Substitute values: $$ P_a + 0 + 0 = (P_a - \rho_a g L) + \frac{1}{2}\rho v^2 + \rho g L $$ Rearranging terms: $$ \rho_a g L - \rho g L = \frac{1}{2}\rho v^2 $$ $$ g L (\rho_a - \rho) = \frac{1}{2}\rho v^2 $$ Solving for $v$: $$ v = \sqrt{\frac{2 g L (\rho_a - \rho)}{\rho}} = \sqrt{\frac{2(10)(10)(1.2 - 1.0)}{1.0}} $$ $$ v = \sqrt{200(0.2)} = \sqrt{40} \approx 6.32 \text{ m/s} $$

Step 3: Calculate the mass flow rate ($\dot{m}$).
$$ \dot{m} = \rho A v $$ Area $A = \frac{\pi d^2}{4} = \frac{3.14 (0.1)^2}{4} = 0.00785 \text{ m}^2$. $$ \dot{m} = (1.0)(0.00785)(\sqrt{40}) \text{ kg/s} $$ Converting to g/s: $$ \dot{m} = 0.00785 \times 6.324 \times 1000 \approx 49.6 \text{ g/s} $$ The precise value is 49.61 g/s.

Bloom Level

Apply

Topic

Fluid Mechanics

Difficulty

3 (Medium)

Ideal Time

120s

Sub-topics

Bernoulli's Principle Mass Flow Rate Ideal Gas Law

PRIMARY SKILL TESTED

Applying Bernoulli's equation to a thermal buoyancy-driven flow problem.

Q.17

When the chimney is closed using a cap at the top, a pressure difference $\Delta P$ develops between the top and the bottom surfaces of the cap. If the changes in the temperature and density of the hot air, due to the stoppage of air flow, are negligible then the value of $\Delta P$ is ______ N m$^{-2}$.

20

Solution

Step 1: Understand the Setup.
The chimney is now closed at the top. The air inside is static. The total height from the open bottom to the closed top is $L = H + h = 10 \text{ m}$.

Step 2: Calculate Pressure Inside at the Top ($P_{in}$).
The pressure at the open bottom is atmospheric pressure $P_a$. Moving up the column of hot air inside the chimney: $$ P_{in} = P_{bottom} - \rho g L $$ $$ P_{in} = P_a - (1.0 \text{ kg/m}^3)(10 \text{ m/s}^2)(10 \text{ m}) = P_a - 100 \text{ Pa} $$

Step 3: Calculate Pressure Outside at the Top ($P_{out}$).
Moving up the column of cold atmospheric air outside: $$ P_{out} = P_{bottom} - \rho_a g L $$ $$ P_{out} = P_a - (1.2 \text{ kg/m}^3)(10 \text{ m/s}^2)(10 \text{ m}) = P_a - 120 \text{ Pa} $$

Step 4: Calculate the Pressure Difference ($\Delta P$).
The pressure difference across the cap is: $$ \Delta P = P_{in} - P_{out} $$ $$ \Delta P = (P_a - 100) - (P_a - 120) $$ $$ \Delta P = 20 \text{ Pa} \text{ or } 20 \text{ N/m}^2 $$

Bloom Level

Apply

Topic

Fluid Mechanics

Difficulty

2 (Easy)

Ideal Time

60s

Sub-topics

Fluid Statics Hydrostatic Pressure

PRIMARY SKILL TESTED

Calculating hydrostatic pressure difference due to density columns of different fluids.

SECTION 1 (Maximum Marks: 12)

This section contains FOUR (04) questions.
Each question has FOUR options (A), (B), (C) and (D). ONLY ONE of these four options is the correct answer.
For each question, choose the option corresponding to the correct answer.
Answer to each question will be evaluated according to the following marking scheme:
Full Marks : +3 If ONLY the correct option is chosen;
Zero Marks : 0 If none of the options is chosen (i.e. the question is unanswered);
Negative Marks : −1 In all other cases.

Q.1

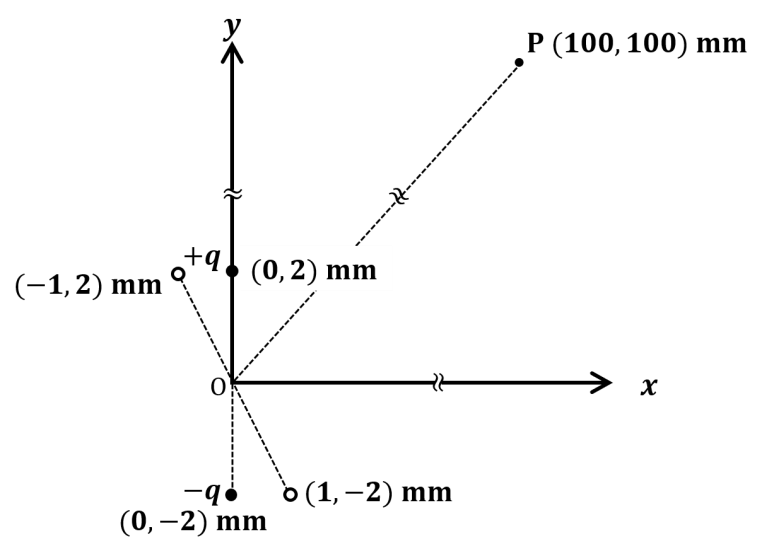
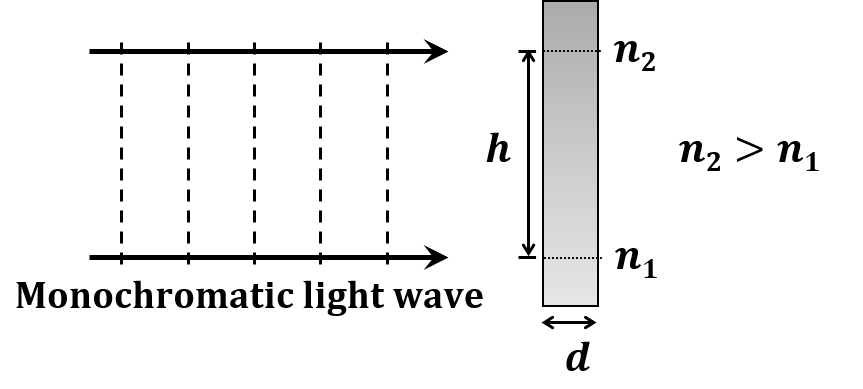
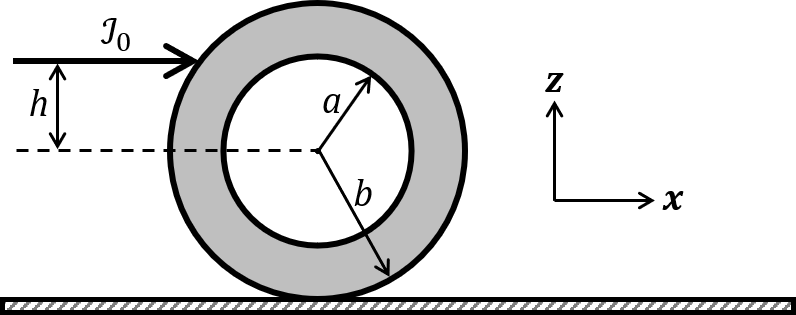
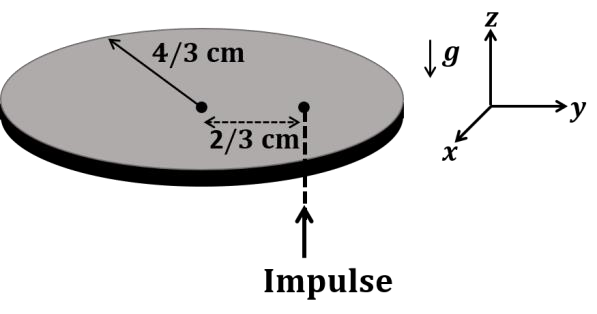
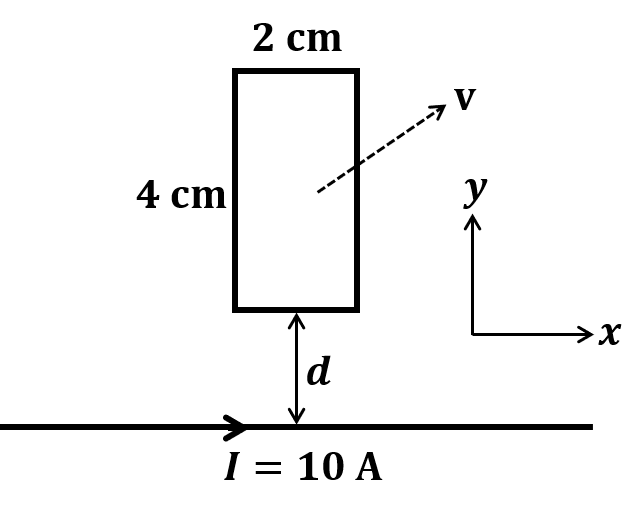
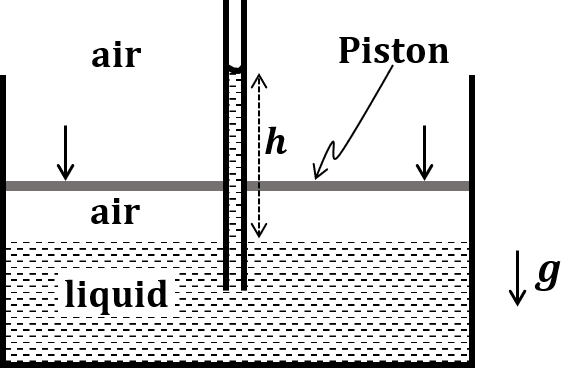
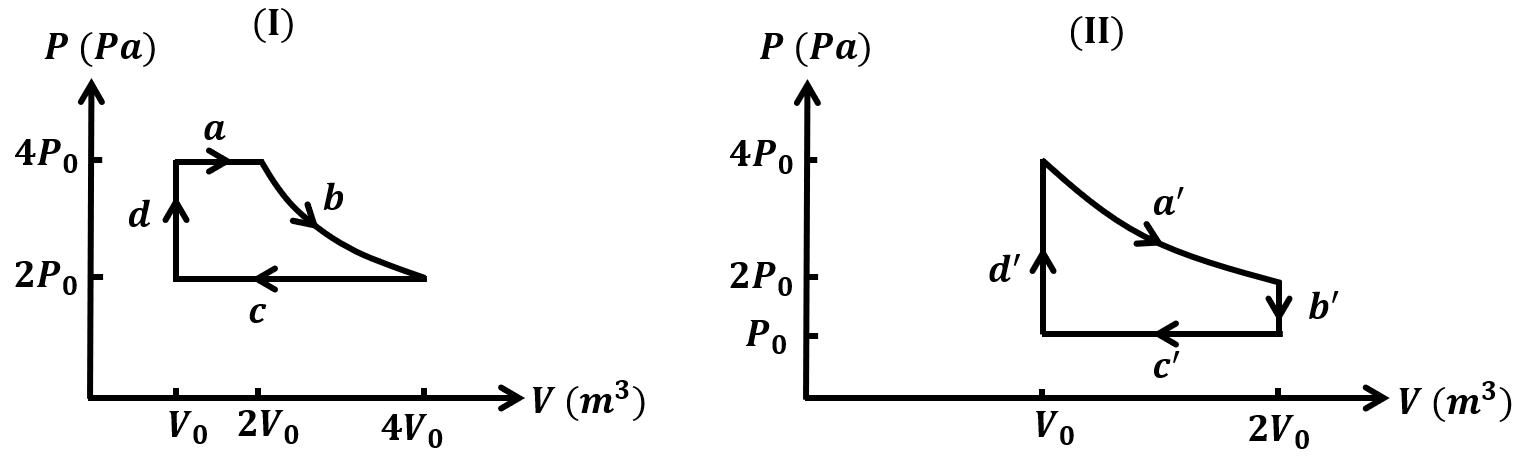
The correct molecular orbital diagram for $\mathrm{F_2}$ molecule in the ground state is: Diagram

(C)

Solution

Step 1: Determine the number of electrons.
The fluorine molecule ($F_2$) is formed by two fluorine atoms. The electronic configuration of a fluorine atom ($Z=9$) is $1s^2 2s^2 2p^5$.
Total valence electrons in $F_2 = 7 + 7 = 14$. (Total electrons = 18).

Step 2: Identify the correct Molecular Orbital (MO) energy ordering.
For diatomic molecules of heavier elements like $O_2$ and $F_2$, the energy difference between the $2s$ and $2p$ atomic orbitals is large enough that $s-p$ mixing is negligible. Consequently, the $\sigma_{2p}$ molecular orbital is lower in energy than the $\pi_{2p}$ orbitals.

The correct energy order for $F_2$ is:
$$ \sigma_{1s} < \sigma^*_{1s} < \sigma_{2s} < \sigma^*_{2s} < \sigma_{2p_z} < \pi_{2p_x}=\ pi_{2p_y} < \pi^*_{2p_x}=\ pi^*_{2p_y} < \sigma^*_{2p_z} $$

Step 3: Fill the electrons into the diagram.
We need to place the 14 valence electrons into the MOs derived from the n=2 shell:

$\sigma_{2s}$ (2 electrons)
$\sigma^*_{2s}$ (2 electrons)
$\sigma_{2p}$ (2 electrons) — Lowest energy 2p MO
$\pi_{2p}$ (4 electrons)
$\pi^*_{2p}$ (4 electrons)

Total valence electrons placed: $2 + 2 + 2 + 4 + 4 = 14$.

Step 4: Analyze the options.

(A) Shows $\pi_{2p}$ below $\sigma_{2p}$, which is the order for $B_2$, $C_2$, and $N_2$. Incorrect for $F_2$.
(B) Shows an incorrect/unconventional ordering.
(C) Shows $\sigma_{2p}$ below $\pi_{2p}$ (correct for $F_2$). It contains 2 electrons in $\sigma_{2s}$, 2 in $\sigma^*_{2s}$, 2 in $\sigma_{2p}$, 4 in $\pi_{2p}$, and 4 in $\pi^*_{2p}$. This correctly accounts for the electrons and energy ordering.
(D) Shows $\pi_{2p}$ below $\sigma_{2p}$. Incorrect.

Therefore, Option (C) is the correct molecular orbital diagram.

Bloom Level

Analyze

Topic

Chemical Bonding

Difficulty

2 (Moderate)

Ideal Time

60 seconds

Sub-topics

Molecular Orbital Theory Homonuclear Diatomic Molecules

PRIMARY SKILL TESTED

Conceptual Understanding of energy level diagrams and electron filling rules.

Option Distractor Reasons

A

Shows the MO diagram for $N_2$ (where $\pi_{2p} < \sigma_{2p}$ due to s-p mixing), which is incorrect for $F_2$.

D

Incorrect energy ordering of orbitals for a heavier diatomic molecule.

Q.2

Consider the following statements related to colloids.

(I) Lyophobic colloids are not formed by simple mixing of dispersed phase and dispersion medium.
(II) For emulsions, both the dispersed phase and the dispersion medium are liquid.
(III) Micelles are produced by dissolving a surfactant in any solvent at any temperature.
(IV) Tyndall effect can be observed from a colloidal solution with dispersed phase having the same refractive index as that of the dispersion medium.

The option with the correct set of statements is

(A)

(I) and (II)

(B)

(II) and (III)

(C)

(III) and (IV)

(D)

(II) and (IV)

(A)

Solution

We evaluate each statement individually:

Statement (I): "Lyophobic colloids are not formed by simple mixing of dispersed phase and dispersion medium."
True. Lyophobic ("solvent-hating") colloids like metal sols are unstable and cannot be formed by simple mixing. They require special methods such as mechanical disintegration, Bredig's arc method, or peptization.
Statement (II): "For emulsions, both the dispersed phase and the dispersion medium are liquid."
True. An emulsion is a colloidal dispersion of a liquid in a liquid (e.g., milk is liquid fat in water).
Statement (III): "Micelles are produced by dissolving a surfactant in any solvent at any temperature."
False. Micelle formation takes place only above a particular temperature called the Kraft temperature ($T_k$) and above a particular concentration called the Critical Micelle Concentration (CMC).
Statement (IV): "Tyndall effect can be observed from a colloidal solution with dispersed phase having the same refractive index as that of the dispersion medium."
False. One of the necessary conditions for the Tyndall effect is that the refractive indices of the dispersed phase and the dispersion medium must differ greatly. If they are the same, light will pass through without scattering.

Therefore, the correct set of statements is (I) and (II).

Bloom Level

Understand

Topic

Surface Chemistry

Difficulty

2 (Moderate)

Ideal Time

90 seconds

Sub-topics

Colloids Emulsions Micelles

PRIMARY SKILL TESTED

Recall and application of properties of colloidal systems.

Option Distractor Reasons

B

Includes Statement III, which is false because micelle formation depends on CMC and Kraft temperature.

C

Includes Statement IV, which is false because Tyndall effect requires a refractive index difference.

Q.3

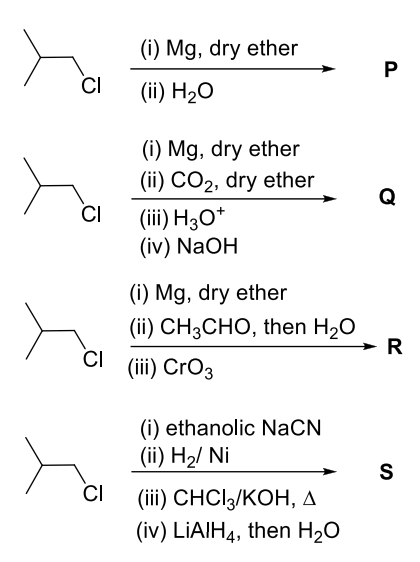In the following reactions, P, Q, R, and S are the major products.

The correct statement about P, Q, R, and S is

(A)

P is a primary alcohol with four carbons.

(B)

Q undergoes Kolbe’s electrolysis to give an eight-carbon product.

(C)

R has six carbons and it undergoes Cannizzaro reaction.

(D)

S is a primary amine with six carbons.

(B)

Solution

The starting material is 1-chloro-2-methylpropane (Isobutyl chloride), $(CH_3)_2CH-CH_2-Cl$. Let's analyze each reaction path:

Path P: 1. $(CH_3)_2CH-CH_2-Cl \xrightarrow{Mg, \text{dry ether}} (CH_3)_2CH-CH_2-MgCl$ (Grignard reagent) 2. $(CH_3)_2CH-CH_2-MgCl \xrightarrow{H_2O} (CH_3)_2CH-CH_3$ (Isobutane)
Analysis of Option A: P is isobutane (an alkane), not a primary alcohol. Option A is Incorrect.

Path Q: 1. Formation of Grignard reagent: $(CH_3)_2CH-CH_2-MgCl$ 2. Reaction with $CO_2$ followed by acid hydrolysis ($H_3O^+$): $$(CH_3)_2CH-CH_2-MgCl + CO_2 \rightarrow (CH_3)_2CH-CH_2-COOMgCl \xrightarrow{H_3O^+} (CH_3)_2CH-CH_2-COOH$$ Product Q is 3-methylbutanoic acid. 3. Analysis of Option B: The option mentions Kolbe's electrolysis. In Kolbe's electrolysis, the salt of the carboxylic acid ($RCOO^-$) undergoes decarboxylation and dimerization to form $R-R$. Here, $R = (CH_3)_2CH-CH_2-$. Dimer $R-R$ is $(CH_3)_2CH-CH_2-CH_2-CH(CH_3)_2$ (2,5-dimethylhexane). Number of carbons = $4 + 4 = 8$. Option B is Correct.

Path R: 1. Grignard reagent reacts with Acetaldehyde ($CH_3CHO$): $$(CH_3)_2CH-CH_2-MgCl + CH_3CHO \rightarrow (CH_3)_2CH-CH_2-CH(OMgCl)-CH_3$$ 2. Hydrolysis: $\rightarrow (CH_3)_2CH-CH_2-CH(OH)-CH_3$ (Secondary Alcohol) 3. Oxidation with $CrO_3$: Secondary alcohol oxidizes to a ketone. $$R = (CH_3)_2CH-CH_2-C(=O)-CH_3$$ Product R is 4-methylpentan-2-one. Analysis of Option C: R has 6 carbons, but it is a ketone. Ketones do not possess the hydrogen on the carbonyl carbon required for the Cannizzaro reaction (which is characteristic of aldehydes without $\alpha$-hydrogens). Option C is Incorrect.

Path S: 1. Nucleophilic substitution with $NaCN$: $$(CH_3)_2CH-CH_2-Cl \xrightarrow{NaCN} (CH_3)_2CH-CH_2-CN \text{ (Nitrile)}$$ 2. Reduction with $H_2/Ni$: $$\rightarrow (CH_3)_2CH-CH_2-CH_2-NH_2 \text{ (Primary Amine)}$$ 3. Carbylamine reaction ($CHCl_3/KOH$): Converts $1^\circ$ amine to Isocyanide. $$\rightarrow (CH_3)_2CH-CH_2-CH_2-NC \text{ (Isocyanide)}$$ 4. Reduction with $LiAlH_4$: Isocyanides are reduced to secondary amines ($R-NH-CH_3$). $$S = (CH_3)_2CH-CH_2-CH_2-NH-CH_3$$ Analysis of Option D: S is a secondary amine, not a primary amine. Option D is Incorrect.

Bloom Level

Evaluate

Topic

Organic Chemistry

Difficulty

4 (Hard)

Ideal Time

180 seconds

Sub-topics

Grignard Reagents Carboxylic Acids Amines Kolbe Electrolysis

PRIMARY SKILL TESTED

Multi-step organic synthesis analysis and reaction mechanism identification.

Option Distractor Reasons

A

P is an alkane (from hydrolysis of Grignard), not a primary alcohol.

C

Product R is a ketone, which cannot undergo the Cannizzaro reaction (restricted to aldehydes without alpha-hydrogens).

D

Reduction of an isocyanide (formed in the previous step) yields a secondary amine ($R-NH-CH_3$), not a primary amine.

Q.4

A disaccharide X cannot be oxidised by bromine water. The acid hydrolysis of X leads to a laevorotatory solution. The disaccharide X is Diagram

(A)

Solution

Step 1: Analyze the properties given.

Property 1: The disaccharide X cannot be oxidised by bromine water. This indicates that X is a non-reducing sugar. It lacks a free aldehyde or ketone group (specifically, the hemiacetal hydroxyl group is not free).
Property 2: Acid hydrolysis of X leads to a laevorotatory solution. This is a characteristic property of Sucrose. Sucrose (dextrorotatory) hydrolyzes to give an equimolar mixture of D-(+)-Glucose (dextrorotatory) and D-(-)-Fructose (strongly laevorotatory). The resulting mixture is laevorotatory, a phenomenon known as "Inversion of cane sugar".

Step 2: Evaluate the structures.

(A) Sucrose: The linkage involves C1 of $\alpha$-D-glucose and C2 of $\beta$-D-fructose. Both anomeric carbons are involved in the glycosidic bond. Thus, it is non-reducing. Its hydrolysis product is invert sugar. This matches all criteria.
(B) This structure shows a glycosidic bond where at least one anomeric carbon might be free or it represents a different disaccharide (like a derivative of trehalose or similar, but the specific structure B is not the common sucrose structure).
(C) & (D) These structures represent disaccharides with at least one free anomeric carbon (hemiacetal group), making them reducing sugars (e.g., Maltose or Cellobiose types). They would be oxidised by bromine water.

Therefore, Option (A) is the correct structure (Sucrose).

Bloom Level

Analyze

Topic

Biomolecules

Difficulty

3 (Moderate)

Ideal Time

60 seconds

Sub-topics

Carbohydrates Disaccharides Reducing Sugars

PRIMARY SKILL TESTED

Identifying carbohydrate structures based on chemical properties (reducing nature and hydrolysis products).

Option Distractor Reasons

C

Shows a reducing sugar (free anomeric OH is available), which would react with bromine water.

D

Shows a reducing sugar (likely maltose or similar), oxidizable by bromine water.

SECTION 2 (Maximum Marks: 12)

This section contains THREE (03) questions.
Each question has FOUR options (A), (B), (C) and (D). ONE OR MORE THAN ONE of these four option(s) is (are) correct answer(s).
Full Marks : +4 ONLY if (all) the correct option(s) is(are) chosen;
Partial Marks : +3 If all the four options are correct but ONLY three options are chosen;
Partial Marks : +2 If three or more options are correct but ONLY two options are chosen, both of which are correct;
Partial Marks : +1 If two or more options are correct but ONLY one option is chosen and it is a correct option;
Zero Marks : 0 If unanswered;
Negative Marks : −2 In all other cases.

Q.5

The complex(es), which can exhibit the type of isomerism shown by $[\mathrm{Pt(NH_3)_2Br_2}]$, is(are)
$[\mathrm{en} = \mathrm{H_2NCH_2CH_2NH_2}]$

(A)

$[\mathrm{Pt(en)(SCN)_2}]$

(B)

$[\mathrm{Zn(NH_3)_2Cl_2}]$

(C)

$[\mathrm{Pt(NH_3)_2Cl_4}]$

(D)

$[\mathrm{Cr(en)_2(H_2O)(SO_4)}]^{+}$

(C), (D)

Solution

The reference complex $[Pt(NH_3)_2Br_2]$ is a square planar complex of the type $MA_2B_2$. It exhibits Geometrical Isomerism (cis and trans forms).

We analyze each option for Geometrical Isomerism (GI):

(A) $[Pt(en)(SCN)_2]$:
- This is a square planar complex involving the bidentate ligand 'en' (ethylenediamine) and two monodentate ligands.
- The bidentate ligand 'en' must occupy adjacent (cis) positions.
- This forces the two SCN ligands to also be in cis positions.
- A trans isomer is not possible because the ethylenediamine chain is not long enough to span trans positions. Thus, it cannot show GI.
(B) $[Zn(NH_3)_2Cl_2]$:
- Zinc ($Zn^{2+}$, $d^{10}$) forms tetrahedral complexes.
- Tetrahedral complexes of the type $MA_2B_2$ do not show geometrical isomerism because all positions are equidistant and equivalent.
(C) $[Pt(NH_3)_2Cl_4]$:
- This is an octahedral complex of the type $MA_2B_4$.
- It can form two isomers:
  - Cis: The two $NH_3$ ligands are adjacent (90°).
  - Trans: The two $NH_3$ ligands are opposite (180°).
- Thus, it shows GI.
(D) $[Cr(en)_2(H_2O)(SO_4)]^+$:
- This is an octahedral complex of the type $[M(AA)_2BC]$.
- It can show geometrical isomerism:
  - Trans: The two monodentate ligands ($H_2O$ and $SO_4$) are trans to each other (180°).
  - Cis: The two monodentate ligands are cis to each other (90°).
- Thus, it shows GI.

The correct options are (C) and (D).

Bloom Level

Analyze

Topic

Coordination Compounds

Difficulty

3 (Moderate)

Ideal Time

90 seconds

Sub-topics

Isomerism Geometrical Isomerism Square Planar vs Tetrahedral

PRIMARY SKILL TESTED

Determining the possibility of geometrical isomerism in different coordination geometries (Tetrahedral, Square Planar, Octahedral).

Option Distractor Reasons

A

Square planar complex with a bidentate ligand ('en') cannot form a trans isomer due to ring strain/span constraints.

B

Tetrahedral complexes do not exhibit geometrical isomerism as all positions relative to one another are identical.

Q.6

Atoms of metals $x, y,$ and $z$ form face-centred cubic (fcc) unit cell of edge length $L_x$, body-centred cubic (bcc) unit cell of edge length $L_y$, and simple cubic unit cell of edge length $L_z$, respectively.

If $r_z = \frac{\sqrt{3}}{2} r_y$ ; $r_y = \frac{8}{\sqrt{3}} r_x$ ; $M_z = \frac{3}{2} M_y$ and $M_z = 3M_x$, then the correct statement(s) is(are)

[Given: $M_x, M_y,$ and $M_z$ are molar masses of metals $x, y,$ and $z$, respectively. $r_x, r_y,$ and $r_z$ are atomic radii of metals $x, y,$ and $z$, respectively.]

(A)

Packing efficiency of unit cell of $x >$ Packing efficiency of unit cell of $y >$ Packing efficiency of unit cell of $z$

(B)

$L_y > L_z$

(C)

$L_x > L_y$

(D)

Density of $x >$ Density of $y$

(A), (B), (D)

Solution

Given Parameters:
1. Structures: $x$ (FCC), $y$ (BCC), $z$ (Simple Cubic).
2. Relations: $r_z = \frac{\sqrt{3}}{2}r_y$ and $r_y = \frac{8}{\sqrt{3}}r_x$.
3. Molar masses: $M_z = \frac{3}{2}M_y = 3M_x$.

Statement (A): Packing Efficiency (P.E.)

$x$ (FCC): P.E. = 74%
$y$ (BCC): P.E. = 68%
$z$ (Simple Cubic): P.E. = 52.4%
Order: $x > y > z$. Statement (A) is correct.

Statement (B): Compare $L_y$ and $L_z$

For $y$ (BCC): Edge length $L_y = \frac{4r_y}{\sqrt{3}}$.
For $z$ (SC): Edge length $L_z = 2r_z$.
Substitute $r_y = \frac{2}{\sqrt{3}}r_z$ (derived from given $r_z = \frac{\sqrt{3}}{2}r_y$): $$L_y = \frac{4}{\sqrt{3}} \left( \frac{2}{\sqrt{3}}r_z \right) = \frac{8}{3}r_z \approx 2.67 r_z$$
Comparing $L_y$ (2.67 $r_z$) with $L_z$ (2 $r_z$): $L_y > L_z$. Statement (B) is correct.

Statement (C): Compare $L_x$ and $L_y$

For $x$ (FCC): $L_x = 2\sqrt{2}r_x$.
Given relation: $r_y = \frac{8}{\sqrt{3}}r_x \Rightarrow r_x = \frac{\sqrt{3}}{8}r_y$.
Substitute $r_x$ into $L_x$: $$L_x = 2\sqrt{2} \left( \frac{\sqrt{3}}{8}r_y \right) = \frac{\sqrt{6}}{4}r_y \approx 0.612 r_y$$
Since $L_y = \frac{4}{\sqrt{3}}r_y \approx 2.309 r_y$.
Clearly, $L_x < L_y$.
The statement says $L_x > L_y$. Statement (C) is incorrect.

Statement (D): Compare Densities ($d_x$ and $d_y$)

Formula: $d = \frac{Z \cdot M}{N_A \cdot L^3}$
Ratio $\frac{d_x}{d_y} = \frac{Z_x M_x}{L_x^3} \times \frac{L_y^3}{Z_y M_y}$
Values:
- $Z_x = 4$ (FCC), $Z_y = 2$ (BCC).
- From mass relation: $M_z = 3M_x$ and $M_z = 1.5M_y \Rightarrow 3M_x = 1.5M_y \Rightarrow M_y = 2M_x$. So $\frac{M_x}{M_y} = \frac{1}{2}$.
- From length calculation in (C): $\frac{L_x}{L_y} = \frac{\sqrt{6}/4}{4/\sqrt{3}} = \frac{\sqrt{18}}{16} = \frac{3\sqrt{2}}{16}$.
- $\frac{L_y}{L_x} = \frac{16}{3\sqrt{2}}$.
Calculation: $$\frac{d_x}{d_y} = \frac{4}{2} \cdot \frac{1}{2} \cdot \left( \frac{16}{3\sqrt{2}} \right)^3 = 1 \cdot \left( \frac{16}{4.24} \right)^3 \approx (3.77)^3 > 1$$
Since ratio > 1, $d_x > d_y$. Statement (D) is correct.

Correct Options: (A), (B), (D)

Bloom Level

Evaluate

Topic

Solid State

Difficulty

4 (Hard)

Ideal Time

180 seconds

Sub-topics

Unit Cell Parameters Packing Efficiency Density of Crystals

PRIMARY SKILL TESTED

Mathematical derivation and comparison of unit cell properties (edge length, density) across different lattice types.

Option Distractor Reasons

C

Calculation reveals that edge length $L_x$ is actually smaller than $L_y$, making the statement $L_x > L_y$ incorrect.

Q.7

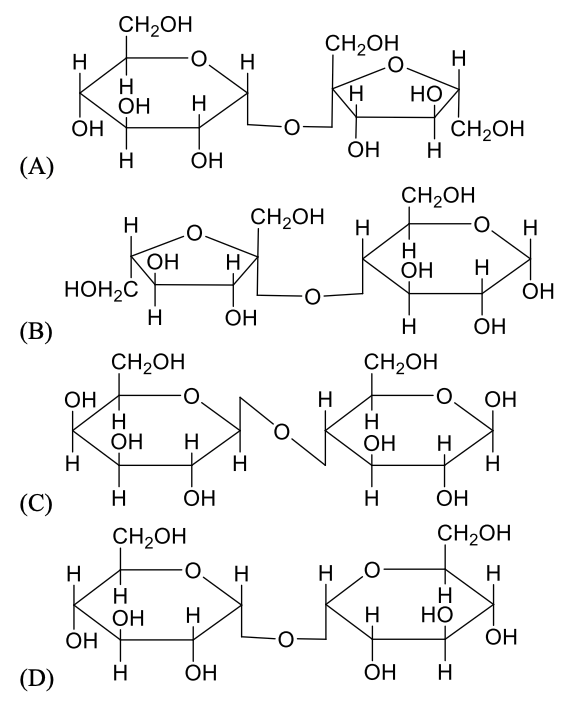
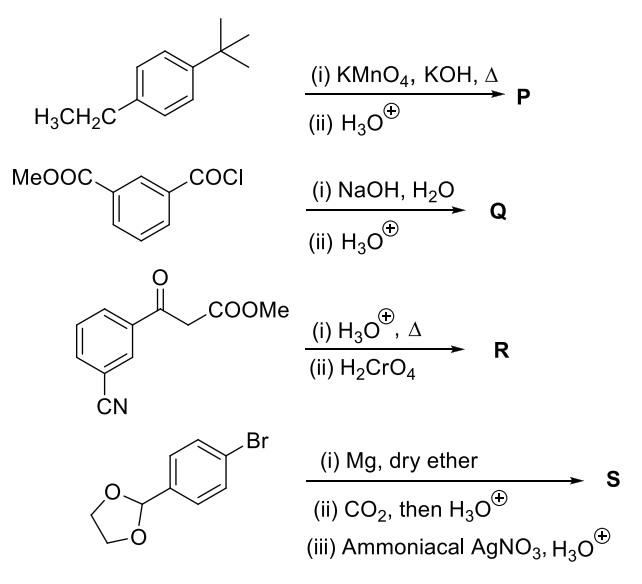In the following reactions, P, Q, R, and S are the major products.

The correct statement(s) about P, Q, R, and S is(are)

(A)

P and Q are monomers of polymers dacron and glyptal, respectively.

(B)

P, Q, and R are dicarboxylic acids.

(C)

Compounds Q and R are the same.

(D)

R does not undergo aldol condensation and S does not undergo Cannizzaro reaction.

(C), (D)

Solution

We analyze the formation of products P, Q, R, and S individually:

Reaction P:
The reactant is 1-ethyl-4-(tert-butyl)benzene.
Reagents: (i) $KMnO_4, KOH, \Delta$ (ii) $H_3O^+$.
$KMnO_4$ is a strong oxidizing agent that oxidizes benzylic alkyl groups containing at least one benzylic hydrogen to a carboxylic acid group ($-\text{COOH}$).
- The ethyl group ($-\text{CH}_2\text{CH}_3$) has benzylic hydrogens and is oxidized to $-\text{COOH}$.
- The tert-butyl group ($-\text{C}(\text{CH}_3)_3$) has no benzylic hydrogens and remains unaffected.
Product P: 4-tert-butylbenzoic acid.

Reaction Q:
The reactant is methyl 3-(chlorocarbonyl)benzoate (an ester-acid chloride).
Reagents: (i) NaOH, H2O (ii) H3O^+.
Basic hydrolysis converts both the acid chloride and the ester groups into carboxylate ions ($-\text{COO}^-$). Acidic workup converts them to carboxylic acids ($-\text{COOH}$).
Product Q: Benzene-1,3-dicarboxylic acid (Isophthalic acid).

Reaction R:
The reactant is methyl 3-(cyanomethylcarbonyl)benzoate derivative.
Reagents: (i) $H_3O^+, \Delta$ (ii) $H_2CrO_4$.
1. Hydrolysis ($H_3O^+$): The nitrile ($-\text{CN}$) hydrolyzes to $-\text{COOH}$, and the ester ($-\text{COOMe}$) hydrolyzes to $-\text{COOH}$.
2. Heating ($\Delta$): The resulting structure contains a $\beta$-keto acid moiety (side chain), which undergoes decarboxylation (loss of $CO_2$). The side chain converts to an acetyl group ($-\text{COCH}_3$).
3. Oxidation ($H_2CrO_4$): Chromic acid is a strong oxidizer. It oxidizes the side chain acetyl group to a carboxylic acid ($-\text{COOH}$).
Product R: Benzene-1,3-dicarboxylic acid (Isophthalic acid).

Reaction S:
The reactant is 2-(3-bromophenyl)-1,3-dioxolane (acetal protected 3-bromobenzaldehyde).
Reagents: (i) Mg, dry ether (ii) $CO_2$, then $H_3O^+$ (iii) Ammoniacal $AgNO_3$, $H_3O^+$.
1. Grignard Formation: $-\text{Br}$ becomes $-\text{MgBr}$.
2. Carbonation: $-\text{MgBr} + CO_2 \rightarrow -\text{COOH}$. Acidic workup ($H_3O^+$) also hydrolyzes the acetal protecting group back to an aldehyde ($-\text{CHO}$).
Intermediate: 3-formylbenzoic acid.
3. Tollens' Reagent (Ammoniacal $AgNO_3$): Oxidizes the aldehyde group ($-\text{CHO}$) to a carboxylate, which upon acidification becomes $-\text{COOH}$.
Product S: Benzene-1,3-dicarboxylic acid (Isophthalic acid).

Analyzing the Options:
(A) P is a monomer of Dacron? False. Dacron requires Terephthalic acid. P is 4-tert-butylbenzoic acid.
(B) P, Q, R are dicarboxylic acids? False. P is a monocarboxylic acid.
(C) Q and R are the same? True. Both are Isophthalic acid.
(D) R does not undergo aldol condensation and S does not undergo Cannizzaro reaction? True. Both R and S are Isophthalic acid. Carboxylic acids do not undergo Aldol or Cannizzaro reactions (these are characteristic of aldehydes/ketones).

Therefore, the correct options are C and D.

Bloom Level

Analyze

Topic

Organic Chemistry

Difficulty

4 (Hard)

Ideal Time

180 seconds

Sub-topics

Oxidation of Hydrocarbons Grignard Reaction Polymers Named Reactions

PRIMARY SKILL TESTED

Multi-step organic synthesis analysis involving oxidation, hydrolysis, and Grignard reagents.

Option Distractor Reasons

A

P is 4-tert-butylbenzoic acid, not Terephthalic acid (the monomer for Dacron).

B

P is a monocarboxylic acid (tert-butyl group resists oxidation), not a dicarboxylic acid.

SECTION 3 (Maximum Marks: 24)

This section contains SIX (06) questions.
The answer to each question is a NON-NEGATIVE INTEGER.
Full Marks : +4 If ONLY the correct integer is entered;
Zero Marks : 0 In all other cases.

Q.8

$\mathrm{H_2S}$ (5 moles) reacts completely with acidified aqueous potassium permanganate solution. In this reaction, the number of moles of water produced is x, and the number of moles of electrons involved is y. The value of (x + y) is ____.

18

Solution

We write and balance the half-reactions for the redox process:

1. Reduction Half-Reaction:
Permanganate ion ($MnO_4^-$) is reduced to Manganese(II) ($Mn^{2+}$) in acidic medium.
$$MnO_4^- + 8H^+ + 5e^- \rightarrow Mn^{2+} + 4H_2O$$ Multiplying by 2 to balance electrons later: $$2MnO_4^- + 16H^+ + 10e^- \rightarrow 2Mn^{2+} + 8H_2O \quad \text{...(i)}$$

2. Oxidation Half-Reaction:
Hydrogen sulfide ($H_2S$) is oxidized to Sulphur ($S$).
$$H_2S \rightarrow S + 2H^+ + 2e^-$$ Multiplying by 5 to equal the electrons in reduction step: $$5H_2S \rightarrow 5S + 10H^+ + 10e^- \quad \text{...(ii)}$$

3. Overall Balanced Equation:
Add (i) and (ii): $$2MnO_4^- + 16H^+ + 5H_2S + 10e^- \rightarrow 2Mn^{2+} + 8H_2O + 5S + 10H^+ + 10e^-$$ Simplifying protons ($16H^+ - 10H^+$): $$2MnO_4^- + 6H^+ + 5H_2S \rightarrow 2Mn^{2+} + 5S + 8H_2O$$

4. Calculation:
Given: 5 moles of $H_2S$ react completely (which matches the coefficient in the balanced equation).

Moles of water produced ($x$): From the equation, 8 moles of $H_2O$ are produced. So, $x = 8$.
Moles of electrons involved ($y$): From the half-reactions, the number of electrons transferred for 5 moles of $H_2S$ is 10. So, $y = 10$.

Final Answer:
Value of $(x + y) = 8 + 10 = 18$.

Bloom Level

Apply

Topic

Physical Chemistry

Difficulty

2 (Moderate)

Ideal Time

90 seconds

Sub-topics

Redox Reactions Stoichiometry Equivalent Concept

PRIMARY SKILL TESTED

Balancing redox reactions by half-reaction method and stoichiometric calculation.

Q.9

Among $[\mathrm{I_3}]^{+}$, $[\mathrm{SiO_4}]^{4-}$, $\mathrm{SO_2Cl_2}$, $\mathrm{XeF_2}$, $\mathrm{SF_4}$, $\mathrm{ClF_3}$, $\mathrm{Ni(CO)_4}$, $\mathrm{XeO_2F_2}$, $[\mathrm{PtCl_4}]^{2-}$, $\mathrm{XeF_4}$, and $\mathrm{SOCl_2}$, the total number of species having $sp^3$ hybridised central atom is ______.

5

Solution

We determine the hybridization of the central atom for each species by counting the Steric Number (SN = Number of Sigma Bonds + Number of Lone Pairs).

$[I_3]^+$ (or $I_2 + I^+$): Central Iodine has 7 valence $e^-$. With a +1 charge, it has 6. It forms 2 bonds with other Iodines.
- Sigma bonds = 2, Lone pairs = $\frac{6-2}{2} = 2$.
- SN = 4 $\Rightarrow$ $sp^3$.
$[SiO_4]^{4-}$: Silicon (Group 14).
- Sigma bonds = 4 (to Oxygen), Lone pairs = 0.
- SN = 4 $\Rightarrow$ $sp^3$.
$SO_2Cl_2$ (Sulfuryl chloride): Sulfur (Group 16).
- Sigma bonds = 4 (2 to O, 2 to Cl), Lone pairs = 0.
- SN = 4 $\Rightarrow$ $sp^3$.
$XeF_2$: Xenon (Group 18).
- Sigma bonds = 2, Lone pairs = 3.
- SN = 5 $\Rightarrow$ $sp^3d$.
$SF_4$: Sulfur (Group 16).
- Sigma bonds = 4, Lone pairs = 1.
- SN = 5 $\Rightarrow$ $sp^3d$.
$ClF_3$: Chlorine (Group 17).
- Sigma bonds = 3, Lone pairs = 2.
- SN = 5 $\Rightarrow$ $sp^3d$.
$Ni(CO)_4$: Nickel(0) is $3d^8 4s^2$. CO is a strong field ligand, forcing pairing of electrons to give $3d^{10} 4s^0$.
- Coordination number = 4. Tetrahedral geometry.
- Hybridization $\Rightarrow$ $sp^3$.
$XeO_2F_2$: Xenon (Group 18).
- Sigma bonds = 4 (2 to O, 2 to F), Lone pairs = 1.
- SN = 5 $\Rightarrow$ $sp^3d$.
$[PtCl_4]^{2-}$: Pt(II) is a $5d^8$ system. With weak field ligand $Cl^-$, but being a $5d$ metal, it forms a square planar complex.
- Hybridization $\Rightarrow$ $dsp^2$.
$XeF_4$: Xenon (Group 18).
- Sigma bonds = 4, Lone pairs = 2.
- SN = 6 $\Rightarrow$ $sp^3d^2$.
$SOCl_2$ (Thionyl chloride): Sulfur (Group 16).
- Sigma bonds = 3 (1 to O, 2 to Cl), Lone pairs = 1.
- SN = 4 $\Rightarrow$ $sp^3$.

Conclusion:
The species with $sp^3$ hybridized central atoms are: $[I_3]^+$, $[SiO_4]^{4-}$, $SO_2Cl_2$, $Ni(CO)_4$, and $SOCl_2$.
Total Count = 5.

Bloom Level

Apply

Topic

Inorganic Chemistry

Difficulty

3 (Moderate)

Ideal Time

120 seconds

Sub-topics

Chemical Bonding Hybridization VSEPR Theory

PRIMARY SKILL TESTED

Determining hybridization states using VSEPR theory and coordination chemistry rules.

Q.10

Consider the following molecules: $\mathrm{Br_3O_8}$, $\mathrm{F_2O}$, $\mathrm{H_2S_4O_6}$, $\mathrm{H_2S_5O_6}$, and $\mathrm{C_3O_2}$.
Count the number of atoms existing in their zero oxidation state in each molecule.
Their sum is____.

6

Solution

We need to determine the oxidation state of atoms in the given molecules based on their structures.

1. $Br_3O_8$ (Tribromooctaoxide):
Structure: $O_3Br-BrO_2-BrO_3$.
- The terminal Bromine atoms are attached to 3 Oxygens each. Oxidation state = +6.
- The central Bromine atom is attached to 2 Oxygens and 2 other Bromines. The bond between identical atoms ($Br-Br$) does not contribute to oxidation state. Thus, the central $Br$ is attached to two oxygens (-2 each). Oxidation state = +4.
- Number of atoms with 0 oxidation state = 0.

2. $F_2O$ (Oxygen difluoride):
Structure: $F-O-F$.
- Fluorine is more electronegative than Oxygen. $F$ has -1, and $O$ has +2.
- Number of atoms with 0 oxidation state = 0.

3. $H_2S_4O_6$ (Tetrathionic acid):
Structure: $HO_3S-S-S-SO_3H$.
- The two terminal Sulfur atoms are in +5 oxidation state.
- The two central Sulfur atoms are bonded only to other Sulfur atoms (S-S bonds). Since there is no electronegativity difference, their oxidation state is 0.
- Number of atoms with 0 oxidation state = 2 (the two central sulfurs).

4. $H_2S_5O_6$ (Pentathionic acid):
Structure: $HO_3S-S-S-S-SO_3H$.
- Similar to tetrathionic acid, the two terminal sulfurs are +5.
- There are three central Sulfur atoms bonded only to other Sulfurs ($S-S-S$). All three have an oxidation state of 0.
- Number of atoms with 0 oxidation state = 3 (the three central sulfurs).

5. $C_3O_2$ (Carbon suboxide):
Structure: $O=C=C=C=O$.
- The two terminal Carbons are bonded to Oxygen (double bond) and another Carbon (double bond). Oxidation state = +2.
- The central Carbon is bonded to two other Carbons. Since it is bonded to identical atoms on both sides, its oxidation state is 0.
- Number of atoms with 0 oxidation state = 1 (the central carbon).

Total Sum:
Sum = $0 (Br_3O_8) + 0 (F_2O) + 2 (H_2S_4O_6) + 3 (H_2S_5O_6) + 1 (C_3O_2)$
Sum = 6.

Bloom Level

Analyze

Topic

Inorganic Chemistry

Difficulty

3 (Moderate)

Ideal Time

120 seconds

Sub-topics

Oxidation States Chemical Bonding Structure of Oxoacids

PRIMARY SKILL TESTED

Assigning oxidation numbers based on molecular structure and bonding connectivity.

Q.11

For $\mathrm{He^+}$, a transition takes place from the orbit of radius 105.8 pm to the orbit of radius 26.45 pm. The wavelength (in nm) of the emitted photon during the transition is ___.

[Use:
Bohr radius, $a = 52.9 \text{ pm}$
Rydberg constant, $R_H = 2.2 \times 10^{-18} \text{ J}$
Planck’s constant, $h = 6.6 \times 10^{-34} \text{ J s}$
Speed of light, $c = 3 \times 10^8 \text{ m s}^{-1}$]

30

Solution

Step 1: Determine the initial and final energy levels ($n_1$ and $n_2$).
The formula for the radius of the $n^{th}$ orbit in a hydrogen-like species is given by: $$r_n = \frac{a_0 \cdot n^2}{Z}$$ where $a_0 = 52.9 \text{ pm}$ and $Z$ is the atomic number. For $He^+$, $Z = 2$.

For the initial orbit ($r_1 = 105.8 \text{ pm}$): $$105.8 = \frac{52.9 \cdot n_1^2}{2}$$ $$n_1^2 = \frac{105.8 \times 2}{52.9} = \frac{211.6}{52.9} = 4 \implies n_1 = 2$$

For the final orbit ($r_2 = 26.45 \text{ pm}$): $$26.45 = \frac{52.9 \cdot n_2^2}{2}$$ $$n_2^2 = \frac{26.45 \times 2}{52.9} = \frac{52.9}{52.9} = 1 \implies n_2 = 1$$ So, the transition is from $n=2$ to $n=1$.

Step 2: Calculate the wavelength ($\lambda$).
Using the Rydberg formula for energy or wavelength: $$\frac{1}{\lambda} = R_H \cdot Z^2 \left( \frac{1}{n_2^2} - \frac{1}{n_1^2} \right)$$ Wait, the given constant is $R_H$ in Joules ($2.2 \times 10^{-18} J$). This is the ionization energy constant. The energy of the photon is: $$\Delta E = R_H Z^2 \left( \frac{1}{n_{final}^2} - \frac{1}{n_{initial}^2} \right)$$ $$\Delta E = 2.2 \times 10^{-18} \cdot (2)^2 \cdot \left( \frac{1}{1^2} - \frac{1}{2^2} \right) \text{ Joules}$$ $$\Delta E = 2.2 \times 10^{-18} \cdot 4 \cdot \left( 1 - 0.25 \right)$$ $$\Delta E = 8.8 \times 10^{-18} \cdot (0.75) = 6.6 \times 10^{-18} \text{ J}$$

Now, find wavelength using $\Delta E = \frac{hc}{\lambda}$: $$\lambda = \frac{hc}{\Delta E}$$ $$\lambda = \frac{(6.6 \times 10^{-34} \text{ J s}) (3 \times 10^8 \text{ m/s})}{6.6 \times 10^{-18} \text{ J}}$$ $$\lambda = \frac{19.8 \times 10^{-26}}{6.6 \times 10^{-18}}$$ $$\lambda = 3 \times 10^{-8} \text{ meters}$$

Convert to nanometers (nm): $$\lambda = 3 \times 10^{-8} \text{ m} \times 10^9 \text{ nm/m} = 30 \text{ nm}$$

Alternative using Rydberg constant in $cm^{-1}$: If one used $R \approx 109677 \text{ cm}^{-1}$, $$\frac{1}{\lambda} = 109677 \times 4 \times \frac{3}{4} \approx 329031 \text{ cm}^{-1}$$ $$\lambda \approx \frac{1}{329031} \text{ cm} \approx 3.039 \times 10^{-6} \text{ cm} = 30.39 \text{ nm}$$ Given the constants provided in the problem ($R_H$ in J), the exact value comes out to 30 nm.

Bloom Level

Apply

Topic

Atomic Structure

Difficulty

2 (Moderate)

Ideal Time

120 seconds

Sub-topics

Bohr Model Electronic Transitions Rydberg Formula

PRIMARY SKILL TESTED

Calculating atomic radius and photon wavelength for electronic transitions in hydrogen-like ions.

Q.12

50 mL of 0.2 molal urea solution (density = $1.012 \text{ g mL}^{-1}$ at 300 K) is mixed with 250 mL of a solution containing 0.06 g of urea. Both the solutions were prepared in the same solvent. The osmotic pressure (in Torr) of the resulting solution at 300 K is ___.

[Use: Molar mass of urea = $60 \text{ g mol}^{-1}$; gas constant, $R = 62 \text{ L Torr K}^{-1} \text{ mol}^{-1}$;
Assume, $\Delta_{mix}H = 0$, $\Delta_{mix}V = 0$]

682

Solution

We need to find the osmotic pressure of the final mixture. Formula: $\Pi = M_{final} R T$.

Step 1: Calculate moles of urea in the first solution (Solution 1).
Given: 50 mL of 0.2 molal solution, Density ($d$) = 1.012 g/mL.
- Mass of solution = Volume × Density = $50 \times 1.012 = 50.6 \text{ g}$.
- Let $n_1$ be moles of urea. Molality ($m$) = 0.2 mol/kg.
$$m = \frac{n_1}{W_{solvent} (kg)}$$ Total mass of solution = $W_{solvent} + W_{solute} = W_{solvent} + (n_1 \times 60)$.
For a larger batch (to find Molarity first or use approximation):
Let's assume 1 kg of solvent. Moles = 0.2. Mass of solution = $1000 + (0.2 \times 60) = 1012 \text{ g}$.
Volume of this batch = $\frac{1012 \text{ g}}{1.012 \text{ g/mL}} = 1000 \text{ mL} = 1 \text{ L}$.
Since 0.2 moles are in 1 L of solution, the Molarity of Solution 1 is 0.2 M.
Now, find moles in 50 mL:
$$n_1 = M_1 \times V_1 = 0.2 \times 0.050 = 0.01 \text{ moles}.$$

Step 2: Calculate moles of urea in the second solution (Solution 2).
Given: 250 mL containing 0.06 g of urea.
- Molar mass of urea = 60 g/mol.
$$n_2 = \frac{0.06}{60} = 0.001 \text{ moles}.$$

Step 3: Calculate final Molarity ($M_{mix}$).
- Total moles ($n_{total}$) = $n_1 + n_2 = 0.01 + 0.001 = 0.011 \text{ moles}$.
- Total Volume ($V_{total}$) = $50 \text{ mL} + 250 \text{ mL} = 300 \text{ mL} = 0.3 \text{ L}$. (Assuming volumes are additive as $\Delta_{mix}V=0$)
$$M_{mix} = \frac{0.011}{0.3} = \frac{11}{300} \text{ mol/L}.$$

Step 4: Calculate Osmotic Pressure ($\Pi$).
Given: $R = 62 \text{ L Torr } K^{-1} mol^{-1}$, $T = 300 \text{ K}$.
$$\Pi = M_{mix} \times R \times T$$ $$\Pi = \frac{11}{300} \times 62 \times 300$$ $$\Pi = 11 \times 62 = 682 \text{ Torr}.$$

Bloom Level

Apply

Topic

Solutions

Difficulty

3 (Moderate)

Ideal Time

150 seconds

Sub-topics

Osmotic Pressure Molarity vs Molality Stoichiometry of Solutions

PRIMARY SKILL TESTED

Calculating concentration (Molarity) from Molality and Density, and applying the Osmotic Pressure formula.

Q.13

The reaction of 4-methyloct-1-ene (P, 2.52 g) with HBr in the presence of $(\mathrm{C_6H_5CO})_2\mathrm{O_2}$ gives two isomeric bromides in a 9 : 1 ratio, with a combined yield of 50%. Of these, the entire amount of the primary alkyl bromide was reacted with an appropriate amount of diethylamine followed by treatment with aq. $\mathrm{K_2CO_3}$ to give a non-ionic product S in 100% yield.

The mass (in mg) of S obtained is ___.

[Use molar mass (in g mol$^{-1}$): H = 1, C = 12, N = 14, Br = 80]

1791

Solution

Step 1: Calculate moles of reactant P.
Reactant P is 4-methyloct-1-ene.
Formula: $CH_2=CH-CH_2-CH(CH_3)-CH_2-CH_2-CH_2-CH_3$.
Molecular Formula: $C_9H_{18}$.
Molar Mass = $(9 \times 12) + (18 \times 1) = 108 + 18 = 126 \text{ g/mol}$.
Moles of P = $\frac{2.52}{126} = 0.02 \text{ mol}$.

Step 2: Analyze the reaction with HBr and Peroxide.
This is the Kharasch effect (Anti-Markovnikov addition). The bromine atom attaches to the less substituted carbon of the double bond.
Major Product (A): 1-bromo-4-methyloctane (Primary bromide).
Minor Product (B): 2-bromo-4-methyloctane (Secondary bromide).
Given Ratio A : B = 9 : 1.

Step 3: Calculate moles of Major Product A.
Total yield is 50%.
Total moles of products = $0.02 \times 0.50 = 0.01 \text{ mol}$.
Moles of A = $\frac{9}{10} \times 0.01 = 0.009 \text{ mol}$.

Step 4: Reaction of A with Diethylamine.
Reaction: $R-CH_2Br + (C_2H_5)_2NH \xrightarrow{K_2CO_3} R-CH_2N(C_2H_5)_2$.
This is a nucleophilic substitution reaction ($S_N2$) yielding a tertiary amine.
Since the yield is 100%, moles of product S = moles of A = 0.009 mol.

Step 5: Calculate mass of Product S.
Product S is N,N-diethyl-4-methyloctan-1-amine.
Structure: $CH_3(CH_2)_3CH(CH_3)(CH_2)_3 - N(C_2H_5)_2$.
Molecular Formula Calculation:

Alkyl chain ($C_9H_{19}$) + Amine part ($N(C_2H_5)_2$).
Total Carbons = $9 + 4 = 13$.
Total Hydrogens = $19 + 10 = 29$.
Total Nitrogens = 1.
Formula: $C_{13}H_{29}N$.

Molar Mass of S = $(13 \times 12) + (29 \times 1) + 14 = 156 + 29 + 14 = 199 \text{ g/mol}$.
Mass of S = Moles $\times$ Molar Mass
Mass = $0.009 \times 199 = 1.791 \text{ g}$.

Step 6: Convert to mg.
Mass = $1.791 \text{ g} = 1791 \text{ mg}$.

Bloom Level

Apply

Topic

Organic Chemistry

Difficulty

3 (Moderate)

Ideal Time

180 seconds

Sub-topics

Stoichiometry Free Radical Addition Amines Preparation

PRIMARY SKILL TESTED

Calculating product yield in a multi-step organic synthesis involving specific reaction mechanisms (Kharasch effect).

SECTION 4 (Maximum Marks: 12)

This section contains TWO (02) paragraphs.
Based on each paragraph, there are TWO (02) questions.
The answer to each question is a NUMERICAL VALUE.
If the numerical value has more than two decimal places, truncate/round-off the value to TWO decimal places.
Full Marks : +3 If ONLY the correct numerical value is entered;
Zero Marks : 0 In all other cases.

“PARAGRAPH I”

The entropy versus temperature plot for phases $\alpha$ and $\beta$ at 1 bar pressure is given. $S_T$ and $S_0$ are entropies of the phases at temperatures T and 0 K, respectively.

The transition temperature for $\alpha$ to $\beta$ phase change is 600 K and $C_{p,\beta} - C_{p,\alpha} = 1 \text{ J mol}^{-1} \text{ K}^{-1}$. Assume $(C_{p,\beta} - C_{p,\alpha})$ is independent of temperature in the range of 200 to 700 K. $C_{p,\alpha}$ and $C_{p,\beta}$ are heat capacities of $\alpha$ and $\beta$ phases, respectively.

Q.14

The value of entropy change, $S_\beta - S_\alpha$ (in $\text{J mol}^{-1} \text{ K}^{-1}$), at 300 K is ___.

[Use: $\ln 2 = 0.69$
Given: $S_\beta - S_\alpha = 0$ at 0 K]

0.31

Solution

Step 1: Extract data from the graph and problem statement.
- $\Delta C_p = C_{p,\beta} - C_{p,\alpha} = 1 \text{ J mol}^{-1} \text{K}^{-1}$.
- From the graph at $T = 600 \text{ K}$ (Transition Temperature): $(S_T - S_0)_\beta = 6$ and $(S_T - S_0)_\alpha = 5$.
- Given $S_\beta - S_\alpha = 0$ at 0 K ($S_{0,\beta} = S_{0,\alpha}$).
- Therefore, the entropy change at 600 K is: $\Delta S_{600} = S_{\beta,600} - S_{\alpha,600} = 6 - 5 = 1 \text{ J mol}^{-1} \text{K}^{-1}$.

Step 2: Use the entropy relation with heat capacity.
The change in entropy difference with temperature is given by: $$ \Delta S_{T_2} - \Delta S_{T_1} = \int_{T_1}^{T_2} \frac{\Delta C_p}{T} dT $$ Here, $T_1 = 300 \text{ K}$ and $T_2 = 600 \text{ K}$. $$ \Delta S_{600} - \Delta S_{300} = \int_{300}^{600} \frac{1}{T} dT $$

Step 3: Perform the calculation.
$$ 1 - \Delta S_{300} = [\ln T]_{300}^{600} $$ $$ 1 - \Delta S_{300} = \ln(600) - \ln(300) = \ln\left(\frac{600}{300}\right) = \ln 2 $$ Given $\ln 2 = 0.69$: $$ 1 - \Delta S_{300} = 0.69 $$ $$ \Delta S_{300} = 1 - 0.69 = 0.31 \text{ J mol}^{-1} \text{K}^{-1} $$

Bloom Level

Analyze

Topic

Thermodynamics

Difficulty

3 (Moderate)

Ideal Time

120 seconds

Sub-topics

Entropy Calculation Phase Transition Temperature Dependence of S

PRIMARY SKILL TESTED

Calculating entropy change at a different temperature using difference in heat capacities ($C_p$).

Q.15

The value of enthalpy change, $H_\beta - H_\alpha$ (in $\text{J mol}^{-1}$), at 300 K is ___.

300

Solution

Step 1: Determine Enthalpy change at Transition Temperature (600 K).
At the transition temperature ($T = 600 \text{ K}$), the phases $\alpha$ and $\beta$ are in equilibrium, so the Gibbs free energy change $\Delta G = 0$.
Using $\Delta G = \Delta H - T \Delta S$: $$ \Delta H_{600} = T \cdot \Delta S_{600} $$ From the previous question solution, we established that $\Delta S_{600} = 1 \text{ J mol}^{-1} \text{K}^{-1}$.
$$ \Delta H_{600} = 600 \text{ K} \times 1 = 600 \text{ J mol}^{-1} $$

Step 2: Apply Kirchhoff's Law to find $\Delta H$ at 300 K.
Kirchhoff's Law relates the enthalpy of reaction at two different temperatures: $$ \Delta H_{T_2} - \Delta H_{T_1} = \int_{T_1}^{T_2} \Delta C_p dT $$ Given $\Delta C_p = 1 \text{ J mol}^{-1} \text{K}^{-1}$ (constant).
$$ \Delta H_{600} - \Delta H_{300} = \Delta C_p (600 - 300) $$ $$ 600 - \Delta H_{300} = 1 \times 300 $$ $$ \Delta H_{300} = 600 - 300 = 300 \text{ J mol}^{-1} $$

Bloom Level

Apply

Topic

Thermodynamics

Difficulty

3 (Moderate)

Ideal Time

90 seconds

Sub-topics

Kirchhoff's Law Gibbs Free Energy Enthalpy Calculation

PRIMARY SKILL TESTED

Application of Kirchhoff's law to calculate enthalpy change at a different temperature.

“PARAGRAPH II”

A trinitro compound, 1,3,5-tris-(4-nitrophenyl)benzene, on complete reaction with an excess of Sn/HCl gives a major product, which on treatment with an excess of $\mathrm{NaNO_2/HCl}$ at $0^\circ\mathrm{C}$ provides P as the product. P, upon treatment with excess of $\mathrm{H_2O}$ at room temperature, gives the product Q. Bromination of Q in aqueous medium furnishes the product R. The compound P upon treatment with an excess of phenol under basic conditions gives the product S.

The molar mass difference between compounds Q and R is $474 \text{ g mol}^{-1}$ and between compounds P and S is $172.5 \text{ g mol}^{-1}$.

Q.16

The number of heteroatoms present in one molecule of R is ______ .

[Use: Molar mass (in g mol$^{-1}$): H = 1, C = 12, N = 14, O = 16, Br = 80, Cl = 35.5
Atoms other than C and H are considered as heteroatoms]

9

Solution

Step 1: Identify the structure of the starting material and intermediate P.
The starting material is 1,3,5-tris-(4-nitrophenyl)benzene.
Reaction with $Sn/HCl$ reduces the nitro groups ($-NO_2$) to amino groups ($-NH_2$).
Reaction with $NaNO_2/HCl$ at $0^\circ C$ converts the amino groups into diazonium salts ($-N_2^+Cl^-$).
So, P is 1,3,5-tris-(4-diazoniophenyl)benzene trichloride.

Step 2: Identify the structure of Q.
Treatment of P with excess $H_2O$ at room temperature causes hydrolysis of the diazonium groups to phenolic hydroxyl groups ($-OH$).
So, Q is 1,3,5-tris-(4-hydroxyphenyl)benzene.

Step 3: Determine the structure of R using quantitative data.
Reaction: Bromination of Q in aqueous medium.
Phenol groups are strongly activating and ortho/para directing. In aqueous bromine, substitution occurs at all available ortho and para positions relative to the -OH group. The para position is already attached to the central benzene ring, so substitution occurs at the ortho positions.
Each phenol ring has 2 ortho positions. With 3 phenol rings, there are potentially $3 \times 2 = 6$ sites for bromination.
Verification with Molar Mass:
Difference in molar mass ($M_R - M_Q$) = $474 \text{ g mol}^{-1}$.
Substitution of one $H$ atom (mass 1) with one $Br$ atom (mass 80) gives a net mass increase of $79 \text{ g mol}^{-1}$.
Number of Bromine atoms = $\frac{474}{79} = 6$.
This confirms that all 6 ortho positions are brominated.
Structure of R: 1,3,5-tris-(3,5-dibromo-4-hydroxyphenyl)benzene.

Step 4: Count the heteroatoms in R.
The molecule R contains:
- 3 Oxygen atoms (from the three -OH groups).
- 6 Bromine atoms (calculated above).
Total number of heteroatoms = $3 \text{ (O)} + 6 \text{ (Br)} = 9$.

Bloom Level

Analyze

Topic

Organic Chemistry

Difficulty

3 (Moderate)

Ideal Time

180 seconds

Sub-topics

Diazonium Salts Electrophilic Aromatic Substitution Phenols

PRIMARY SKILL TESTED

Deducing chemical structures from reaction sequences and quantitative molar mass data.

Q.17

The total number of carbon atoms and heteroatoms present in one molecule of S is ______ .

[Use: Molar mass (in g mol$^{-1}$): H = 1, C = 12, N = 14, O = 16, Br = 80, Cl = 35.5
Atoms other than C and H are considered as heteroatoms]

51

Solution

Step 1: Identify the reaction forming S.
Product P (tris-diazonium salt) is treated with excess phenol under basic conditions. This is an Azo Coupling Reaction.
The diazonium cation ($Ar-N_2^+$) acts as an electrophile and attacks the electron-rich phenol ring, typically at the para-position.
Reaction: $R-N_2^+Cl^- + C_6H_5OH \xrightarrow{OH^-} R-N=N-C_6H_4-OH \text{ (para-hydroxyazo compound)}$.
Since P has three diazonium groups, it couples with three phenol molecules.

Step 2: Verify with Molar Mass Data.
Molar mass difference between S and P is given as $172.5 \text{ g mol}^{-1}$.
Let's check the mass change per functional group:
- Reactant group in P: $-N_2^+ Cl^-$ (Mass $\approx 28 + 35.5 = 63.5$)
- Product group in S: $-N=N-C_6H_4-OH$ (Mass $\approx 28 + 76 + 17 = 121$)
- Net change per arm = $121 - 63.5 = 57.5 \text{ g/mol}$.
- Total change for 3 arms = $3 \times 57.5 = 172.5 \text{ g/mol}$.
This perfectly matches the given data, confirming the formation of the tris-azo dye structure.

Step 3: Count Carbon atoms and Heteroatoms in S.
Structure of S: 1,3,5-tris(4-[(4-hydroxyphenyl)azo]phenyl)benzene.
The molecule consists of:

Central benzene ring: 6 Carbon atoms.
Three linker phenyl rings: $3 \times 6 = 18$ Carbon atoms.
Three terminal phenol rings: $3 \times 6 = 18$ Carbon atoms.
Three Azo groups ($-N=N-$): $3 \times 2 = 6$ Nitrogen atoms.
Three Hydroxyl groups ($-OH$): $3 \times 1 = 3$ Oxygen atoms.

Calculation:
- Total Carbon atoms = $6 + 18 + 18 = 42$.
- Total Heteroatoms = $6 \text{ (Nitrogens)} + 3 \text{ (Oxygens)} = 9$.
- Grand Total = $42 + 9 = 51$.

Bloom Level

Evaluate

Topic

Organic Chemistry

Difficulty

3 (Moderate)

Ideal Time

180 seconds

Sub-topics

Azo Coupling Stoichiometry Structure Elucidation

PRIMARY SKILL TESTED

Calculating molecular formula based on synthesis steps and mass difference validation.