Solution
Step 1: Analyze the Limit Condition
Given the limit: \[ \lim_{t \to x} \frac{t^{10}f(x) - x^{10}f(t)}{t^9 - x^9} = 1 \] Substituting \( t = x \), we get the form \( \frac{x^{10}f(x) - x^{10}f(x)}{x^9 - x^9} = \frac{0}{0} \). Since it is an indeterminate form, we
can apply L'Hospital's Rule by differentiating the numerator and denominator with respect to \( t \) (treating \( x \) as a constant).
Step 2: Apply L'Hospital's Rule
\[ \lim_{t \to x} \frac{\frac{d}{dt}(t^{10}f(x) - x^{10}f(t))}{\frac{d}{dt}(t^9 - x^9)} = 1 \] \[ \lim_{t \to x} \frac{10t^9 f(x) - x^{10}f'(t)}{9t^8} = 1 \] Now, substitute the limit \( t = x \): \[ \frac{10x^9 f(x) - x^{10}f'(x)}{9x^8}
= 1 \] Simplify the expression by canceling \( x^8 \) from the numerator and denominator: \[ \frac{x(10f(x) - xf'(x))}{9} = 1 \] \[ 10xf(x) - x^2 f'(x) = 9 \] Rearranging to form a linear differential equation: \[ x^2 f'(x) - 10x
f(x) = -9 \]
Step 3: Solve the Linear Differential Equation
Divide the entire equation by \( x^2 \) to isolate \( f'(x) \): \[ f'(x) - \frac{10}{x}f(x) = -\frac{9}{x^2} \] This is a linear differential equation of the form \( f'(x) + P(x)f(x) = Q(x) \), where \( P(x) = -\frac{10}{x} \).
Find the Integrating Factor (I.F.): \[ \text{I.F.} = e^{\int P(x) dx} = e^{\int -\frac{10}{x} dx} = e^{-10 \ln x} = e^{\ln (x^{-10})} = x^{-10} = \frac{1}{x^{10}} \]
Multiply the differential equation by the I.F.: \[ \frac{d}{dx} \left( f(x) \cdot \frac{1}{x^{10}} \right) = -\frac{9}{x^2} \cdot \frac{1}{x^{10}} = -9x^{-12} \] Integrate both sides with respect to \( x \): \[ \frac{f(x)}{x^{10}} = \int -9x^{-12} dx \] \[ \frac{f(x)}{x^{10}} = -9 \frac{x^{-11}}{-11} + C \] \[ \frac{f(x)}{x^{10}} = \frac{9}{11}x^{-11} + C \] \[ f(x) = \frac{9}{11x} + C x^{10} \]
Step 4: Determine the Constant C
Use the initial condition \( f(1) = 2 \): \[ f(1) = \frac{9}{11(1)} + C(1)^{10} = 2 \] \[ \frac{9}{11} + C = 2 \] \[ C = 2 - \frac{9}{11} = \frac{22 - 9}{11} = \frac{13}{11} \]
Step 5: Final Function
Substitute \( C \) back into the function expression: \[ f(x) = \frac{9}{11x} + \frac{13}{11}x^{10} \] Comparing this with the given options, this matches the structure of Option (B)
Option Distractor Reasons
Likely result of a sign error during integration or rearranging the differential equation.
Swaps the coefficients of the terms \( \frac{1}{x} \) and \( x^{10} \).
Incorrect signs on the terms.
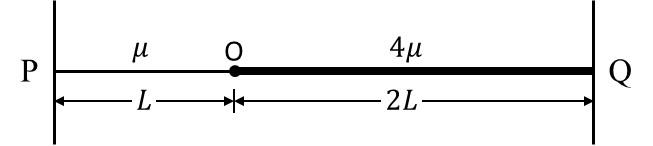
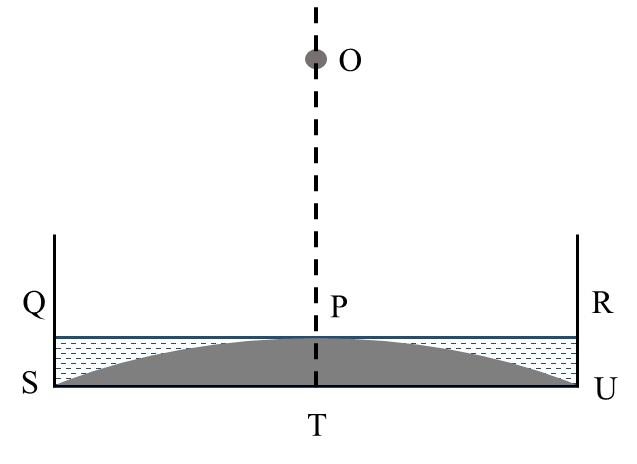
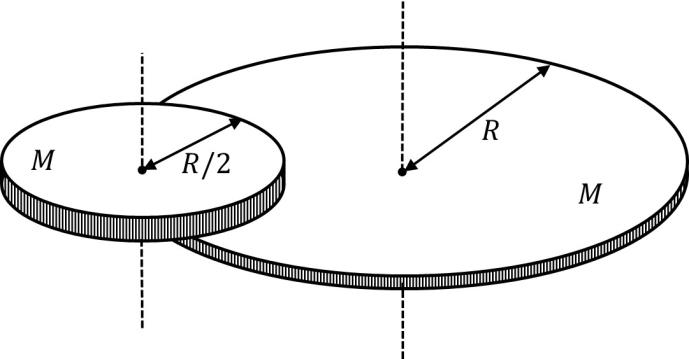
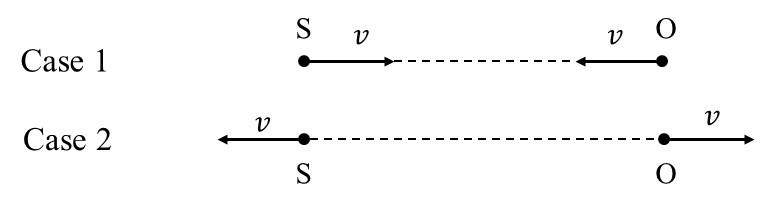
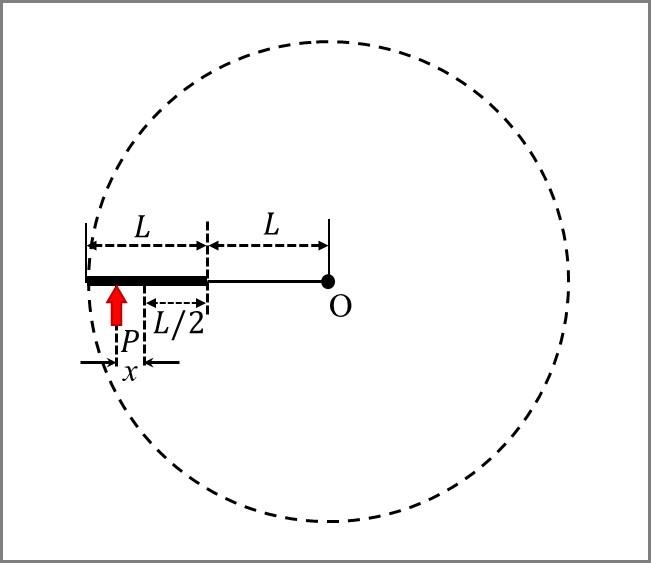
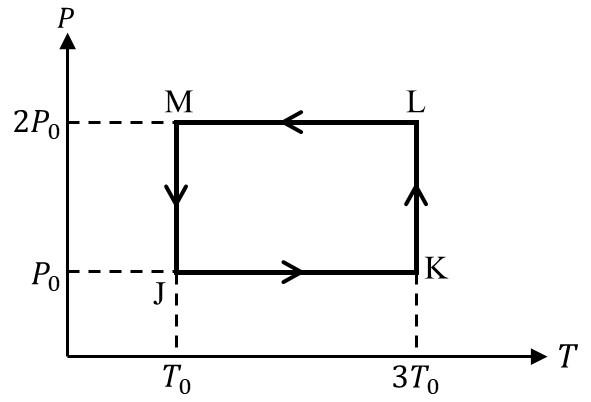
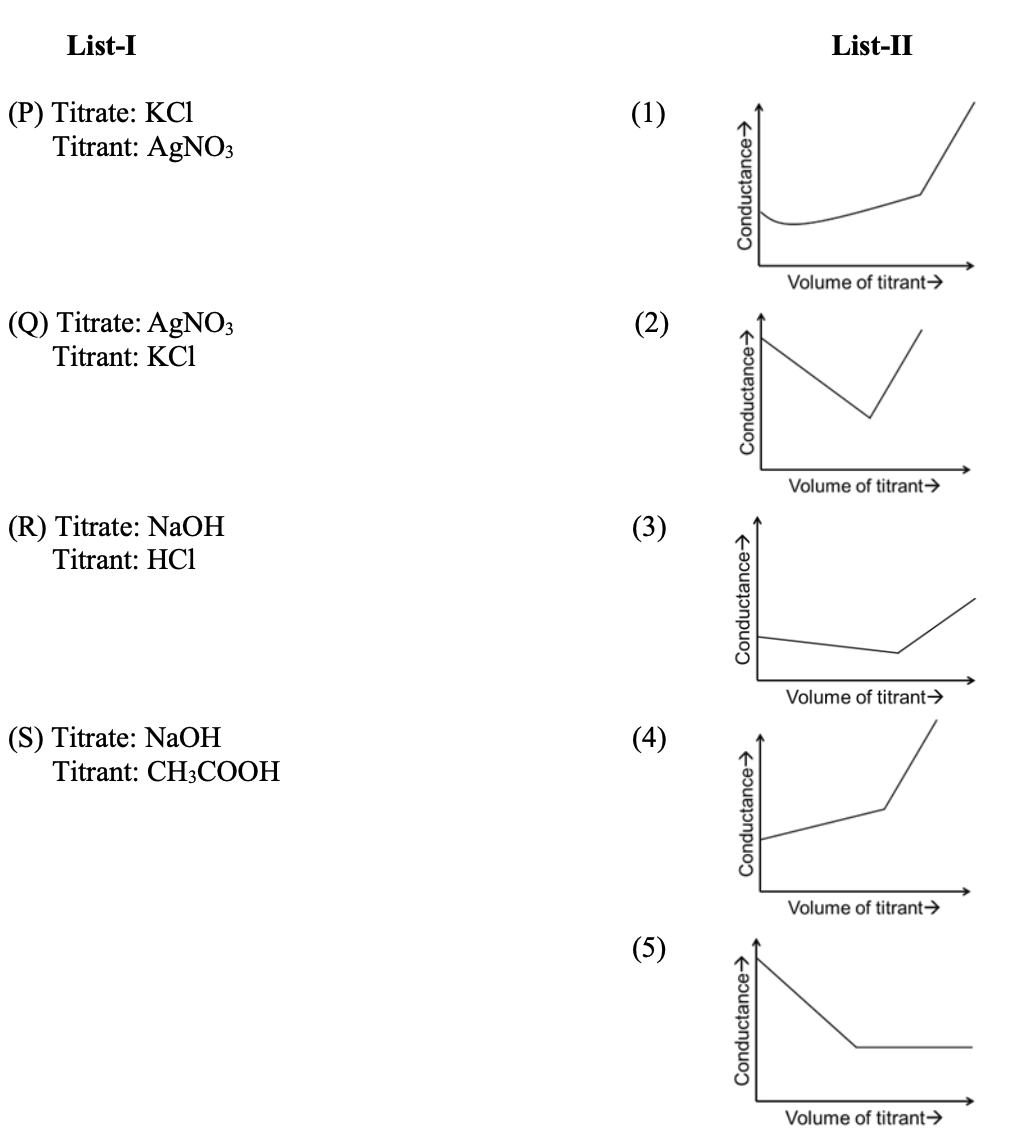
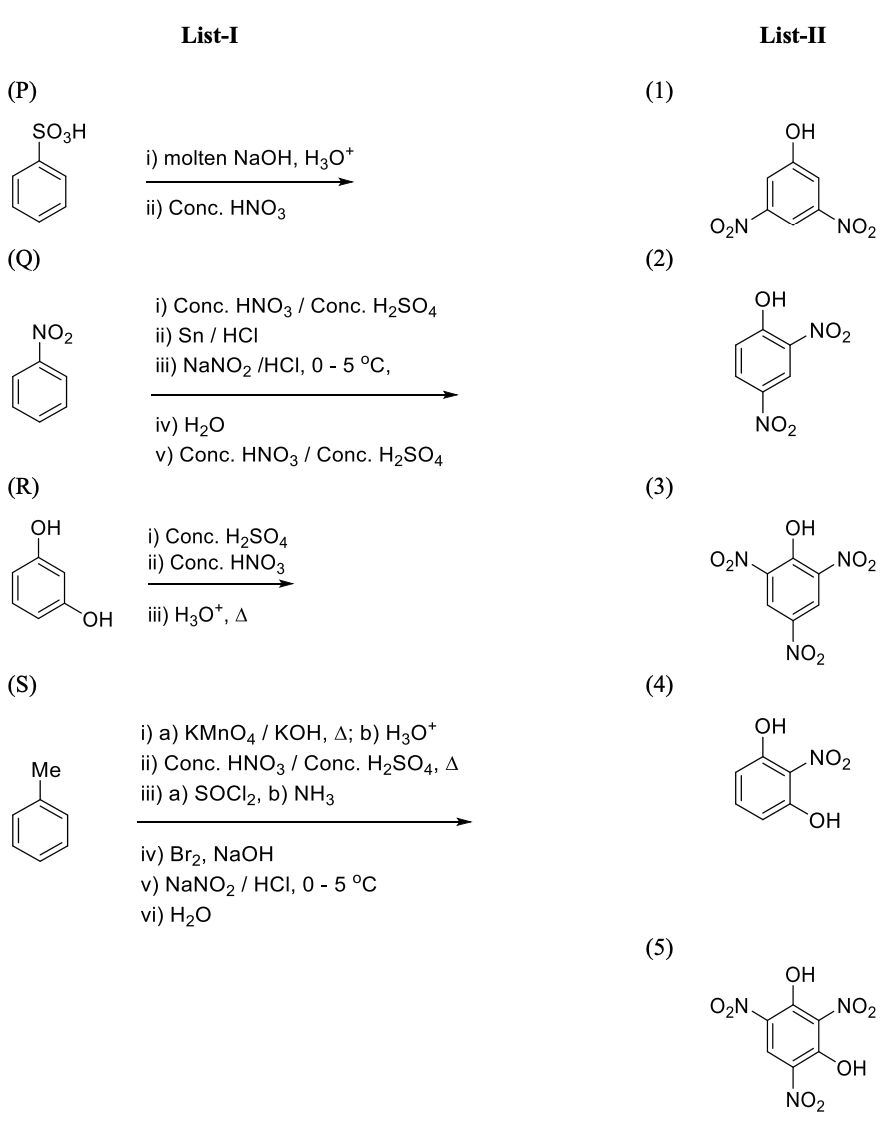
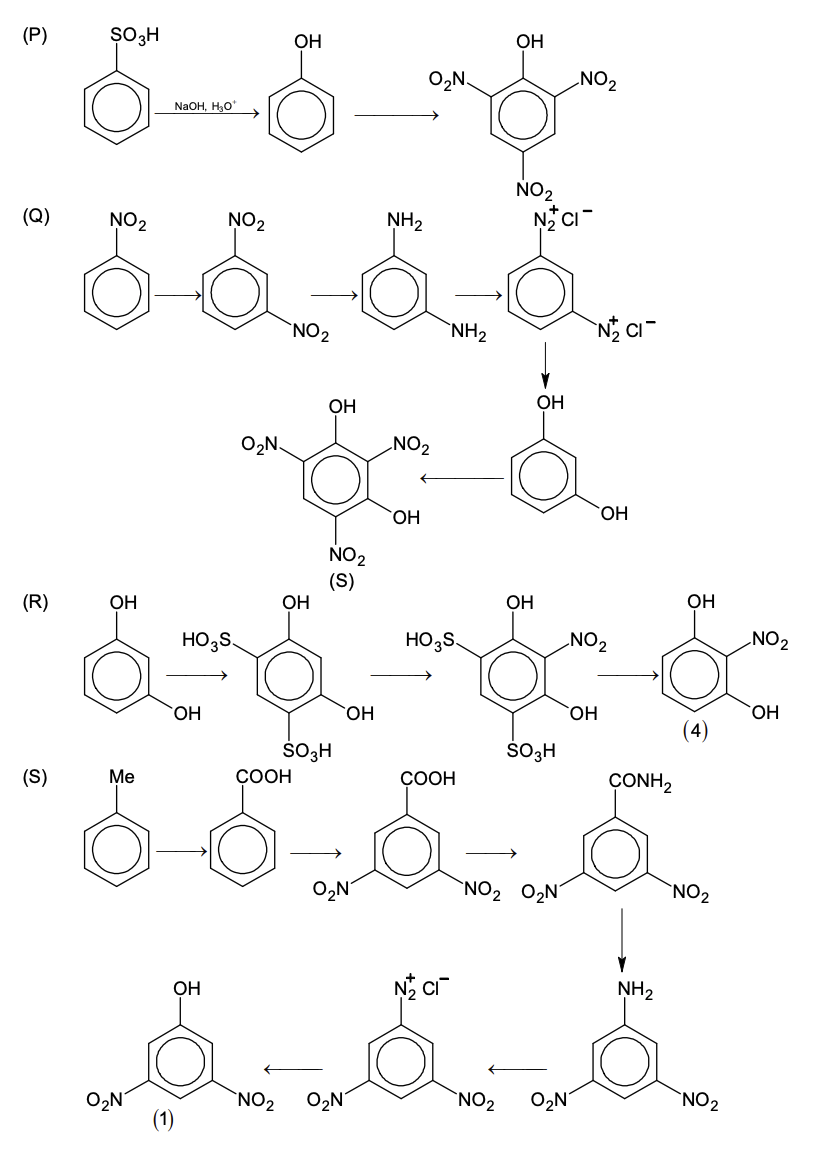
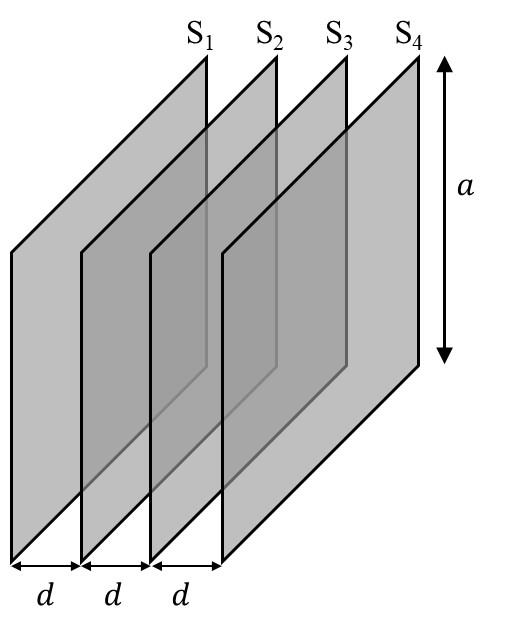 Match the quantities mentioned in List-I with their values in List-II and choose the correct
option.
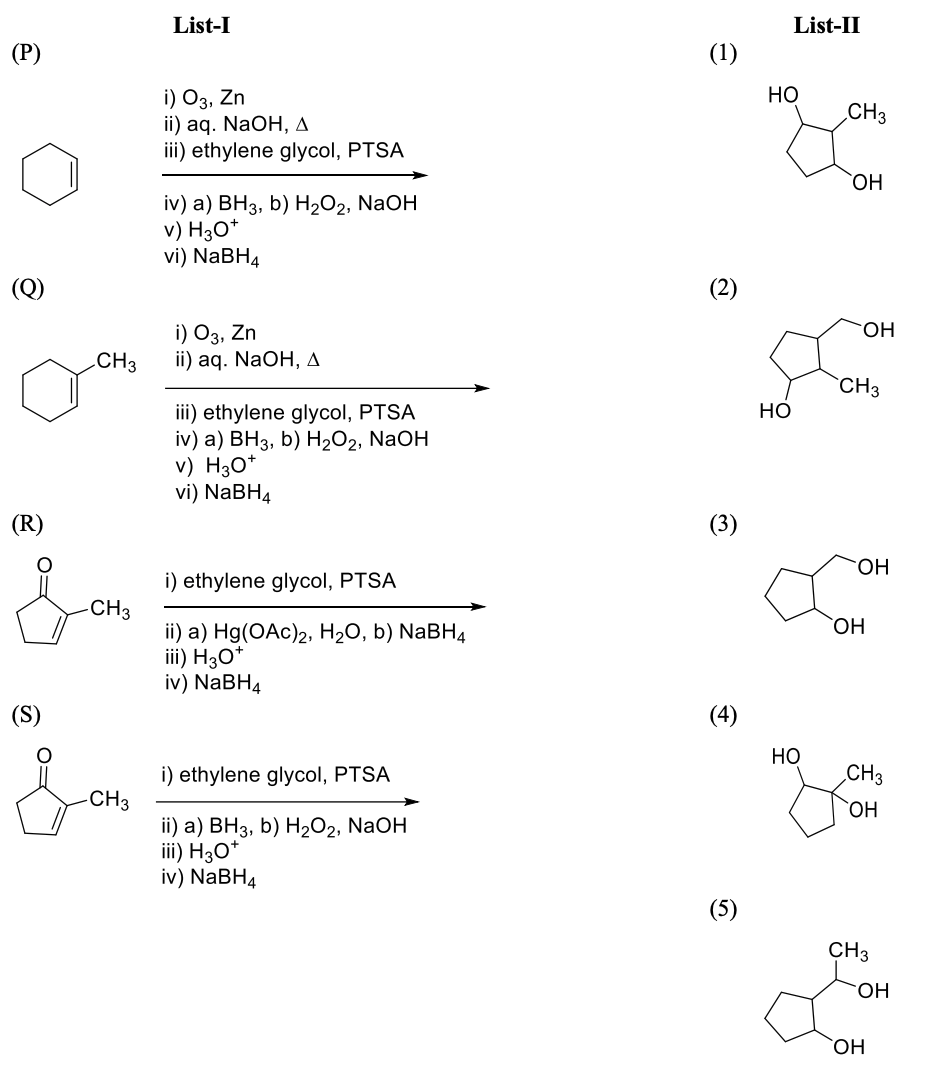
Match the quantities mentioned in List-I with their values in List-II and choose the correct
option.
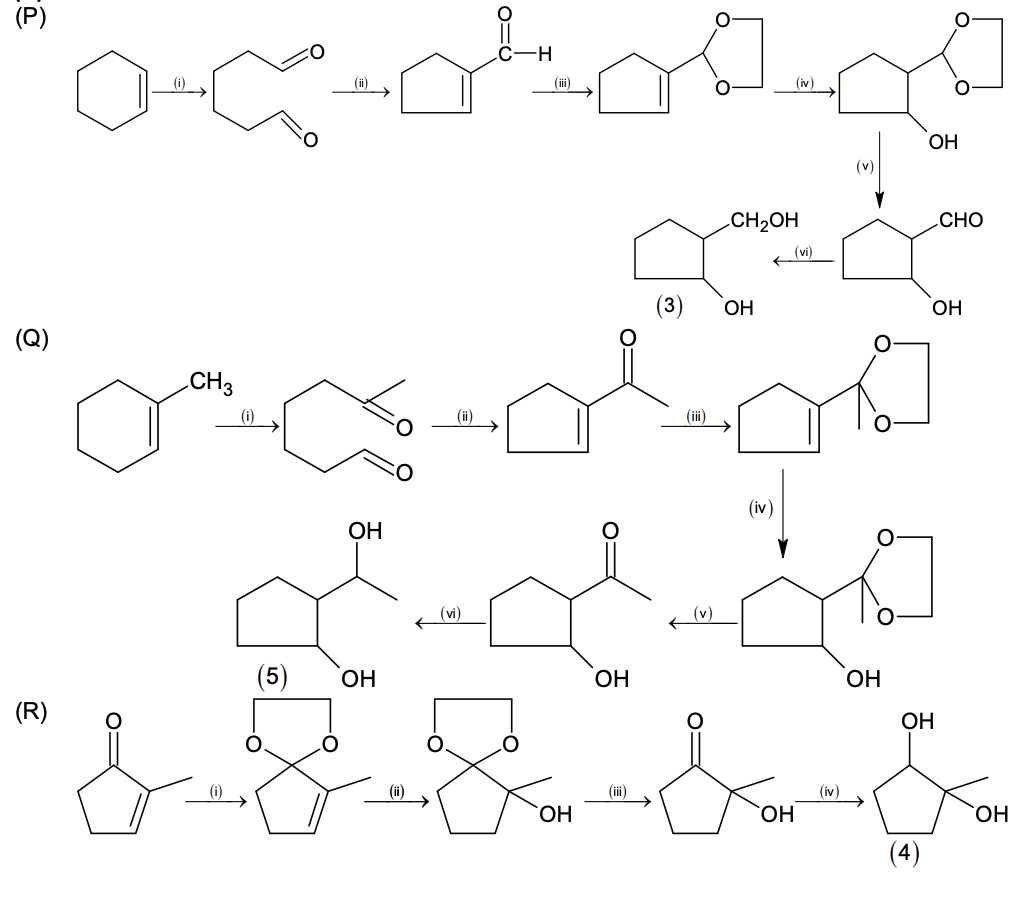
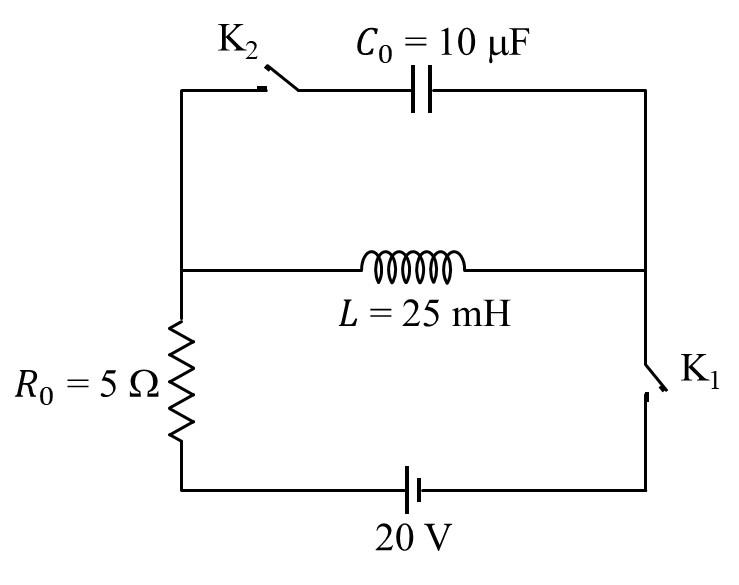 Match the quantities mentioned in List-I with their values in List-II and choose the correct
option.
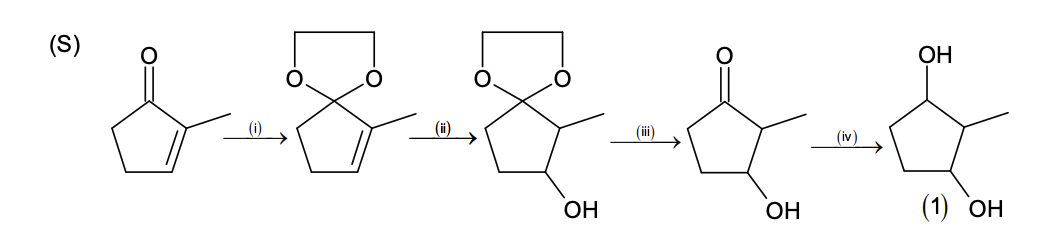
Match the quantities mentioned in List-I with their values in List-II and choose the correct
option.
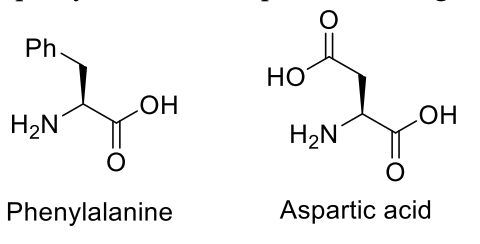
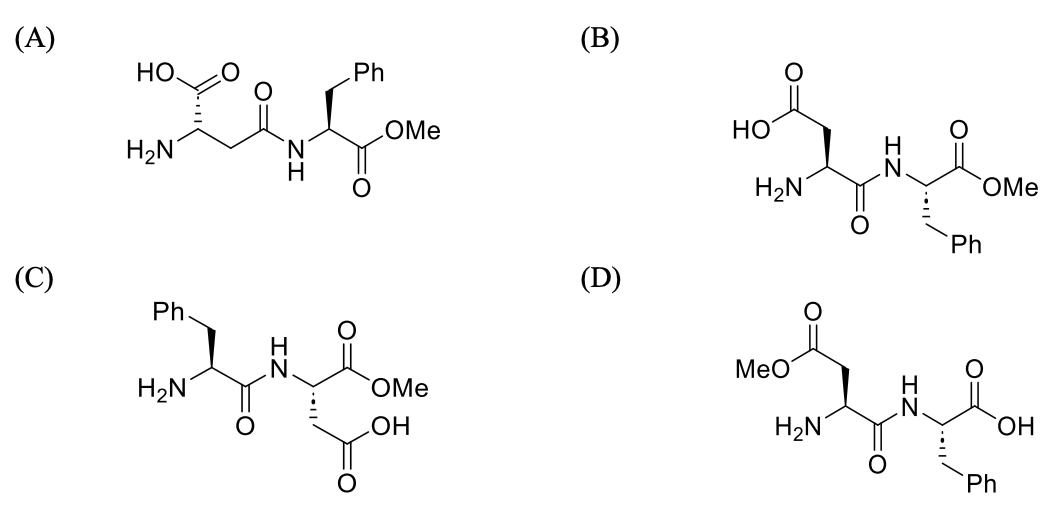
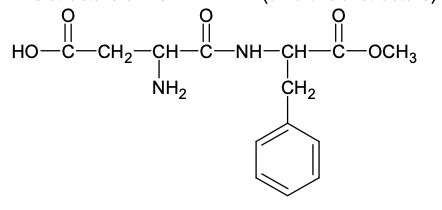

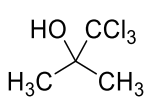
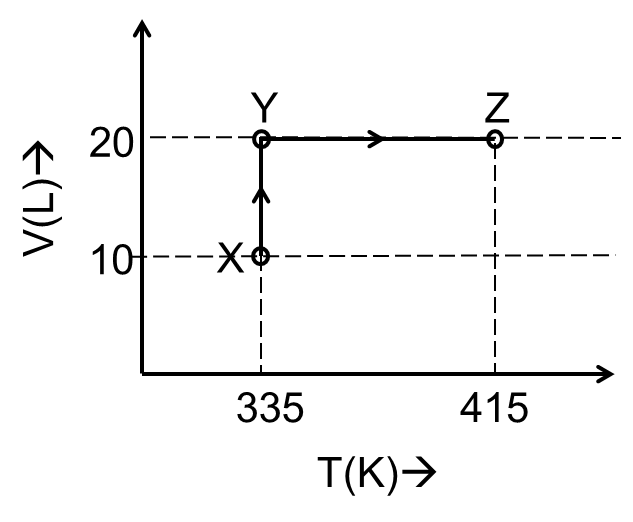 Considering only P-V work is involved, the total change in enthalpy (in Joule) for the
transformation of state in the sequence $\textbf{X} \to \textbf{Y} \to \textbf{Z}$ is
______.
Considering only P-V work is involved, the total change in enthalpy (in Joule) for the
transformation of state in the sequence $\textbf{X} \to \textbf{Y} \to \textbf{Z}$ is
______.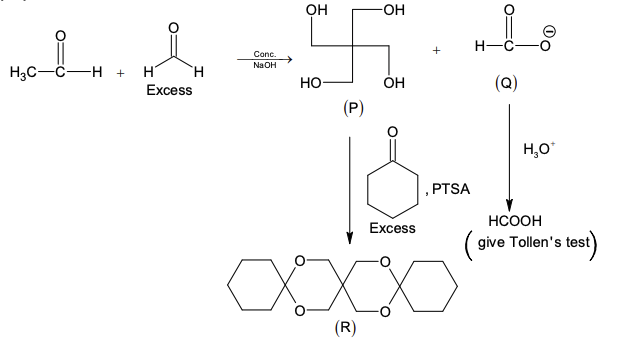
 Glycerol reacts completely with excess $\textbf{P}$ in the presence of an acid catalyst to
form $\textbf{Q}$. Reaction of $\textbf{Q}$ with excess NaOH followed by the treatment with
$\text{CaCl}_2$ yields Ca-soap $\textbf{R}$, quantitatively.
Starting with one mole of $\textbf{Q}$, the amount of $\textbf{R}$ produced in gram is
______.
Glycerol reacts completely with excess $\textbf{P}$ in the presence of an acid catalyst to
form $\textbf{Q}$. Reaction of $\textbf{Q}$ with excess NaOH followed by the treatment with
$\text{CaCl}_2$ yields Ca-soap $\textbf{R}$, quantitatively.
Starting with one mole of $\textbf{Q}$, the amount of $\textbf{R}$ produced in gram is
______.