Solution
We need to find the value of:
$$ \tan\left(\sin^{-1}\left(\frac{3}{5}\right) - 2\cos^{-1}\left(\frac{2}{\sqrt{5}}\right)\right) $$Step 1: Convert inverse trigonometric functions to $\tan^{-1}$.
For $\sin^{-1}\left(\frac{3}{5}\right)$, consider a right-angled triangle with perpendicular $3$ and hypotenuse $5$. The base is $\sqrt{5^2 - 3^2} = 4$.
$$ \therefore \sin^{-1}\left(\frac{3}{5}\right) = \tan^{-1}\left(\frac{3}{4}\right) $$For $\cos^{-1}\left(\frac{2}{\sqrt{5}}\right)$, consider a triangle with base $2$ and hypotenuse $\sqrt{5}$. The perpendicular is $\sqrt{(\sqrt{5})^2 - 2^2} = \sqrt{5-4} = 1$.
$$ \therefore \cos^{-1}\left(\frac{2}{\sqrt{5}}\right) = \tan^{-1}\left(\frac{1}{2}\right) $$Step 2: Substitute these values back into the expression.
$$ \text{Expression} = \tan\left( \tan^{-1}\frac{3}{4} - 2\tan^{-1}\frac{1}{2} \right) $$Step 3: Simplify the term $2\tan^{-1}\frac{1}{2}$.
Using the formula $2\tan^{-1}x = \tan^{-1}\left(\frac{2x}{1-x^2}\right)$:
$$ 2\tan^{-1}\left(\frac{1}{2}\right) = \tan^{-1}\left( \frac{2 \times \frac{1}{2}}{1 - (\frac{1}{2})^2} \right) = \tan^{-1}\left( \frac{1}{1 - \frac{1}{4}} \right) = \tan^{-1}\left( \frac{1}{3/4} \right) = \tan^{-1}\left(\frac{4}{3}\right) $$Step 4: Evaluate the final expression.
$$ \text{Expression} = \tan\left( \tan^{-1}\frac{3}{4} - \tan^{-1}\frac{4}{3} \right) $$Using the formula $\tan(A - B) = \frac{\tan A - \tan B}{1 + \tan A \tan B}$, where $A = \tan^{-1}\frac{3}{4}$ and $B = \tan^{-1}\frac{4}{3}$:
$$ = \frac{\frac{3}{4} - \frac{4}{3}}{1 + \left(\frac{3}{4}\right)\left(\frac{4}{3}\right)} $$ $$ = \frac{\frac{9 - 16}{12}}{1 + 1} $$ $$ = \frac{-7/12}{2} = \frac{-7}{24} $$Thus, the value is $\frac{-7}{24}$.
Option Distractor Reasons
Likely sign error in the numerator of the subtraction formula ($3/4 - 4/3$).
Potential arithmetic error during fraction simplification ($9-16 \neq -5$).
Incorrect sign and arithmetic calculation.
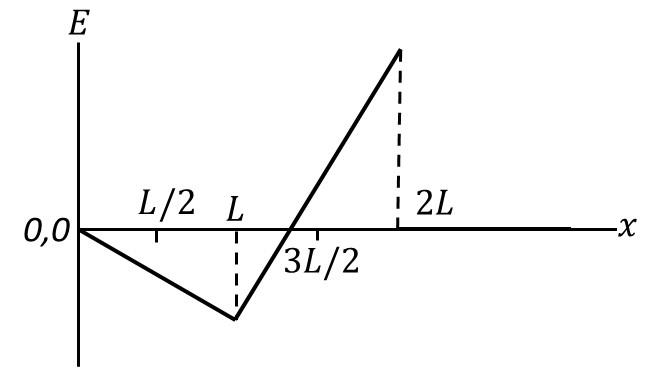
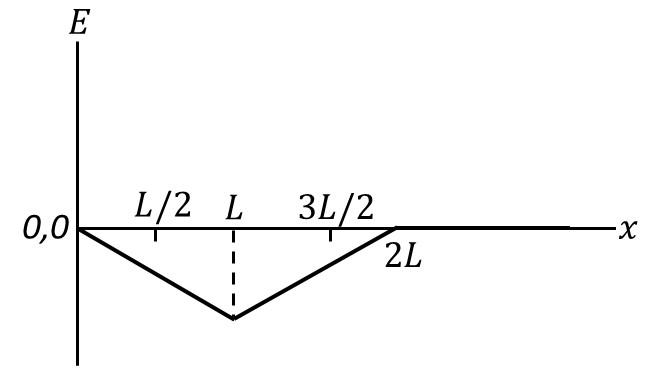
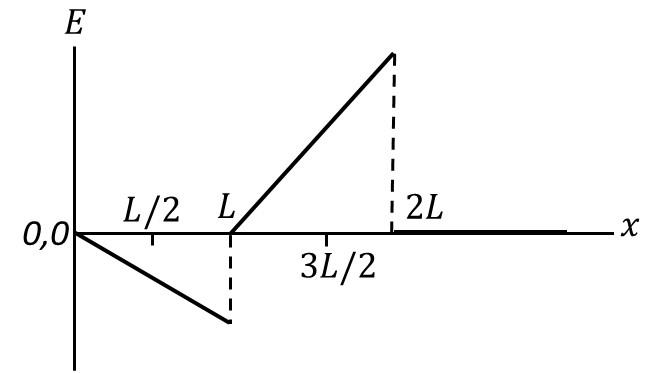
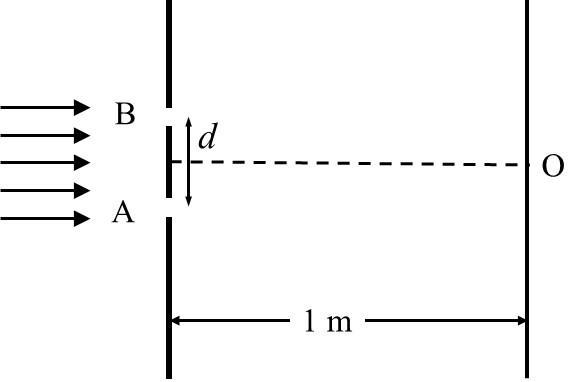
 Which of the following graph best depicts the variation of the induced emf ($E$) in the loop
as a function of the distance ($x$) starting from $x = 0$?
Which of the following graph best depicts the variation of the induced emf ($E$) in the loop
as a function of the distance ($x$) starting from $x = 0$?


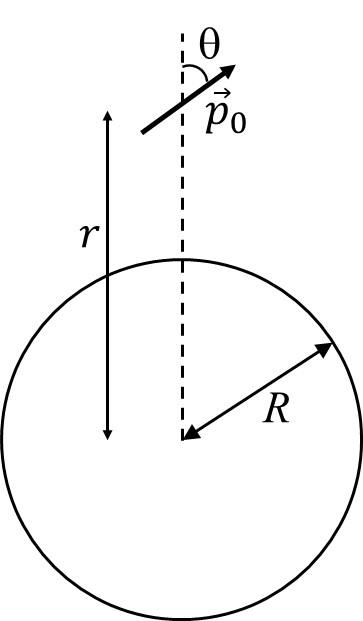 If released from rest, then which of the following statement(s) is(are) correct?
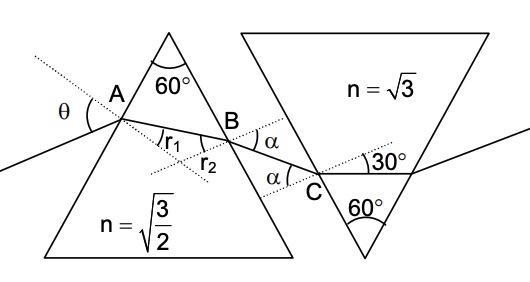
If released from rest, then which of the following statement(s) is(are) correct? Which of the following option(s) is(are) correct?
Which of the following option(s) is(are) correct?


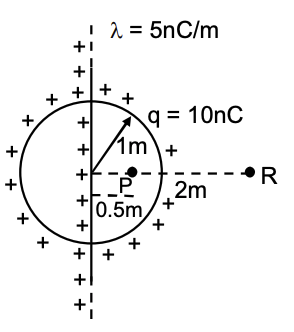
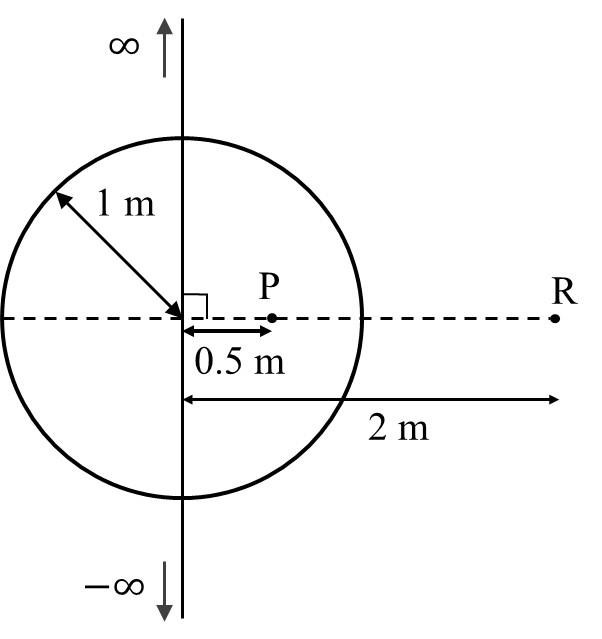 [Given: In SI units $\frac{1}{4\pi\epsilon_0} = 9 \times 10^9$, $\ln 2 = 0.7$. Ignore the
area pierced by the wire.]
[Given: In SI units $\frac{1}{4\pi\epsilon_0} = 9 \times 10^9$, $\ln 2 = 0.7$. Ignore the
area pierced by the wire.]

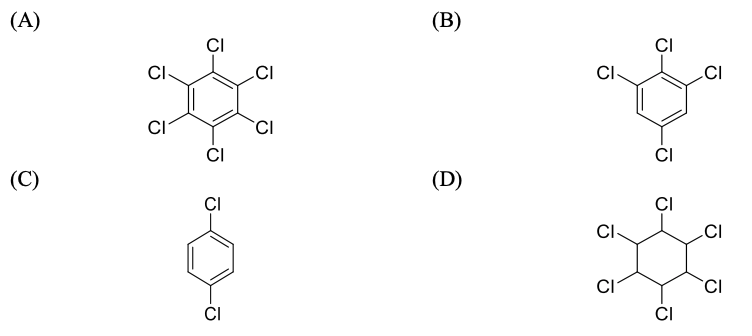
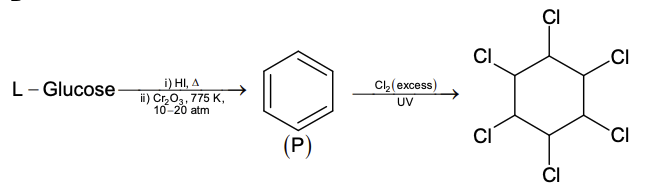
 The amount of energy required to split the double strand DNA into two single strands is
_____ kcal $mol^{-1}$.
The amount of energy required to split the double strand DNA into two single strands is
_____ kcal $mol^{-1}$.