Solution
1. Define Coordinates and Constraint:
Let $\theta$ be the angular displacement of the center of mass (CM) of the disk from the vertical equilibrium line.
Let $\beta$ be the angle of rotation of the disk about its center.
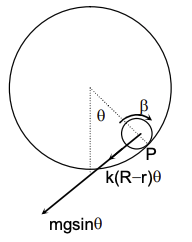
For rolling without slipping, the arc length moved by the CM along the ring must equal the arc length rotated by the disk: $$ (R-r)\theta = r\beta $$ $$ \implies \theta = \frac{r}{R-r}\beta $$
2. Analysis of Forces and Torque:
We analyze the motion using the torque equation about the Instantaneous Axis of Rotation (IAOR), which is the point of contact $P$ between the disk and the ring.
The moment of inertia of the disk about the point of contact $P$ is given by the Parallel Axis Theorem: $$ I_P = I_{CM} + mr^2 = \frac{1}{2}mr^2 + mr^2 = \frac{3}{2}mr^2 $$
There are two restoring forces providing torque about $P$:
1. Gravity: Acts downwards at the center of the disk. The component perpendicular to the radius $R-r$ is $mg \sin \theta \approx mg\theta$ (for small angles). The lever arm from $P$ is $r$. $$ \tau_g = - (mg\theta)r
$$ 2. Spring Force: The spring is attached to the center of the disk. The extension of the spring corresponds to the linear displacement of the center: $x = (R-r)\theta$. The spring force is $F_s = kx = k(R-r)\theta$.
This force acts tangentially. The lever arm from $P$ is $r$. $$ \tau_s = - F_s r = - [k(R-r)\theta]r $$
3. Equation of Motion:
Applying Newton's Second Law for rotation $\tau_{net} = I_P \alpha_{disk}$, where $\alpha_{disk} = \ddot{\beta}$ is the angular acceleration of the disk: $$ I_P \ddot{\beta} = \tau_g + \tau_s $$ $$ \frac{3}{2}mr^2 \ddot{\beta}
= - mgr\theta - kr(R-r)\theta $$ Substitute $\theta = \frac{r}{R-r}\beta$ into the equation: $$ \frac{3}{2}mr^2 \ddot{\beta} = - \left[ mgr\left( \frac{r}{R-r}\beta \right) + kr(R-r)\left( \frac{r}{R-r}\beta \right) \right] $$
Simplify the terms: $$ \frac{3}{2}mr^2 \ddot{\beta} = - \left[ \frac{mgr^2}{R-r}\beta + kr^2\beta \right] $$ Cancel $mr^2$ from both sides: $$ \frac{3}{2} \ddot{\beta} = - \left[ \frac{g}{R-r} + \frac{k}{m} \right] \beta $$ $$
\ddot{\beta} = - \frac{2}{3} \left[ \frac{g}{R-r} + \frac{k}{m} \right] \beta $$
4. Conclusion:
This is the standard equation for Simple Harmonic Motion (SHM) of the form $\ddot{\beta} = - \omega^2 \beta$. Comparing the terms, we get the square of the angular frequency: $$ \omega^2 = \frac{2}{3} \left( \frac{g}{R-r} + \frac{k}{m}
\right) $$ Taking the square root: $$ \omega = \sqrt{\frac{2}{3} \left( \frac{g}{R-r} + \frac{k}{m} \right)} $$ This matches Option (A).
Option Distractor Reasons
Incorrectly separates the spring term from the rotational inertia factor (2/3), treating the spring contribution as independent of the disk's rotational mass.
Uses an incorrect coefficient (1/6), which likely arises from errors in calculating the moment of inertia or applying the parallel axis theorem.
Uses an incorrect coefficient (1/4), likely resulting from algebraic errors or incorrect geometry assumptions during derivation.







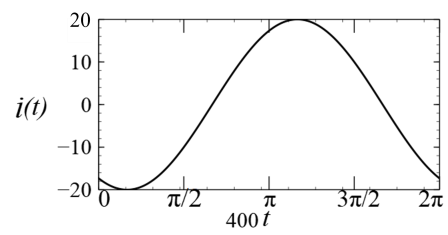

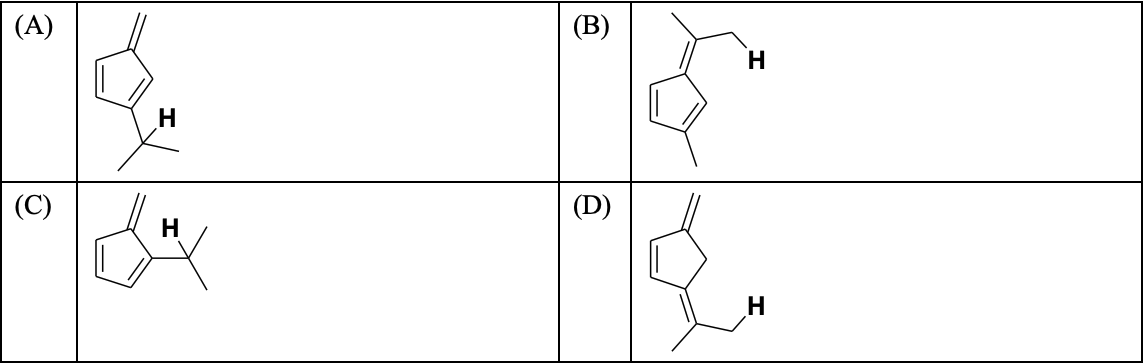
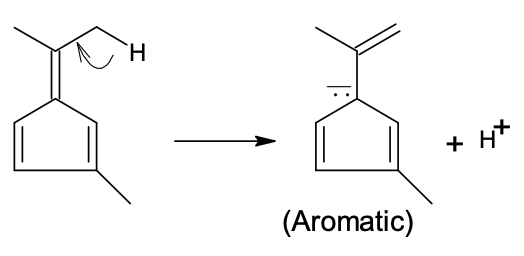
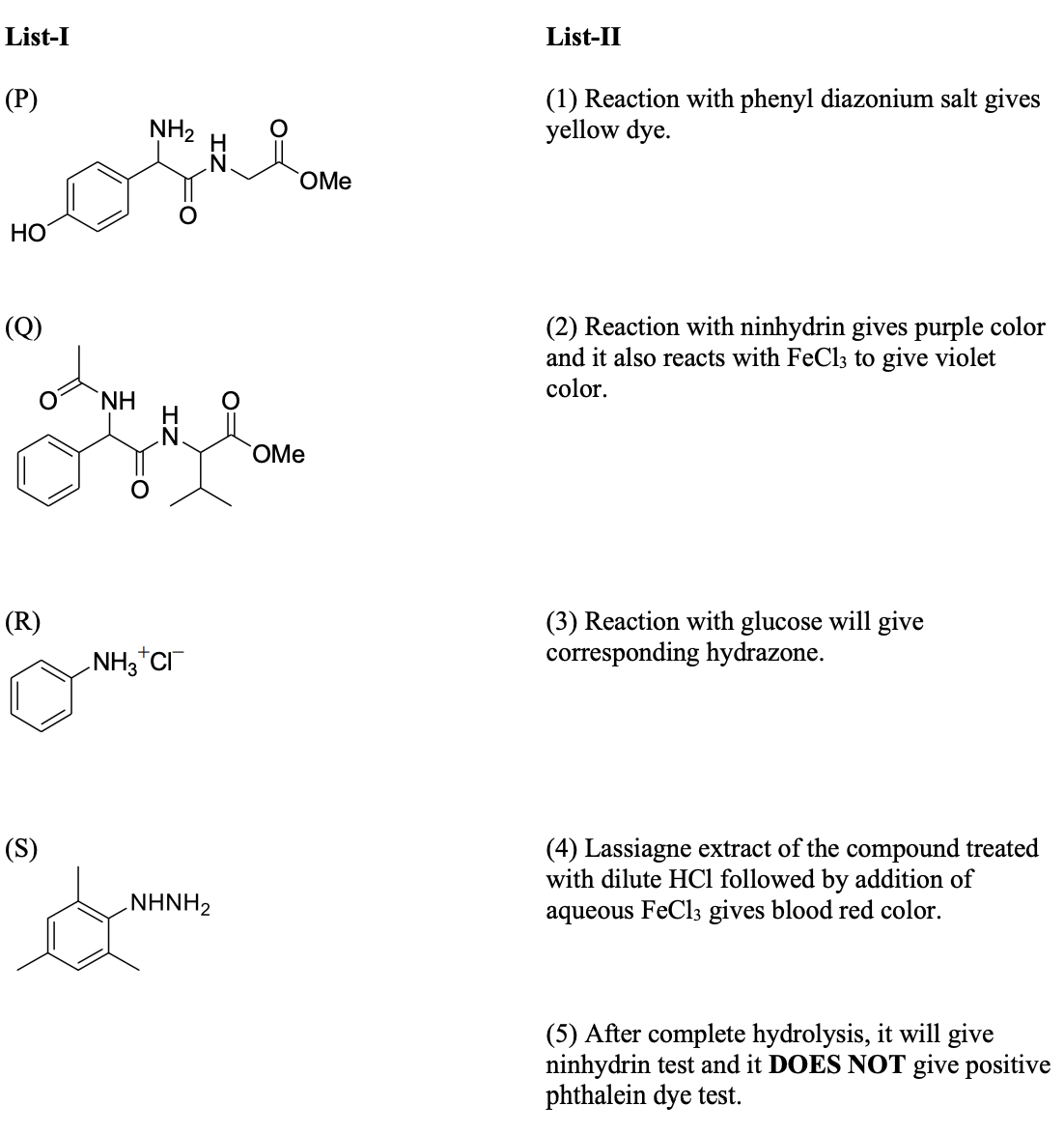
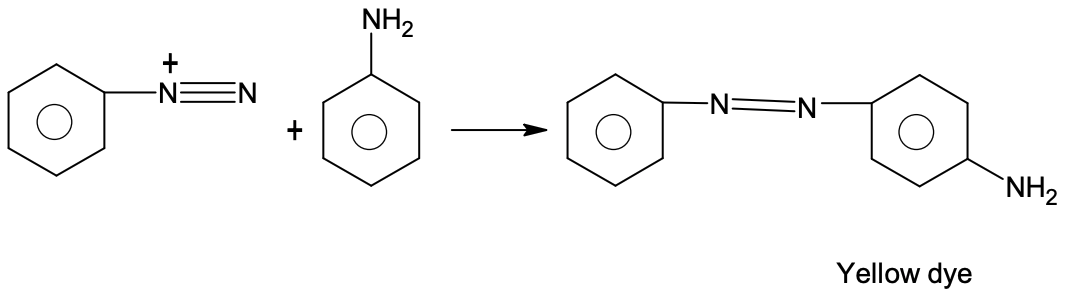
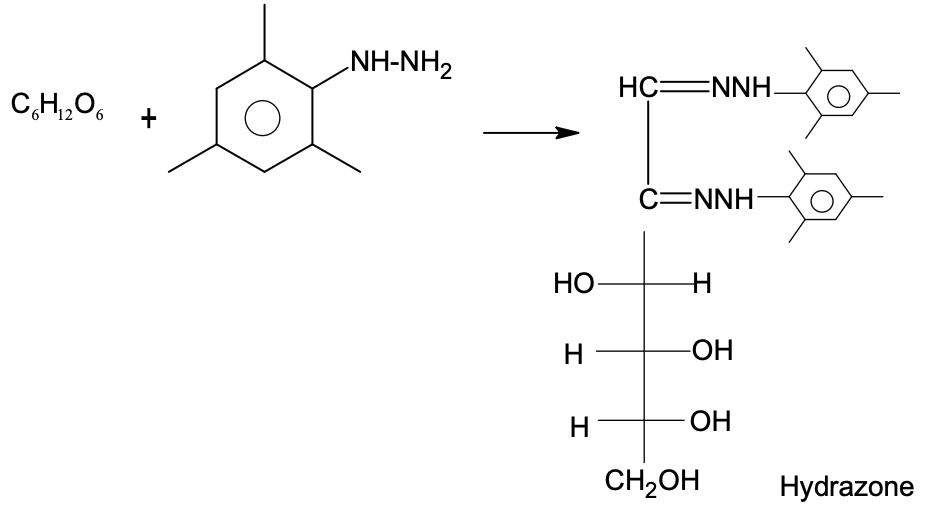
 (In the options, X
is any atom other than carbon and hydrogen, and it is different in P, Q
and R)
(In the options, X
is any atom other than carbon and hydrogen, and it is different in P, Q
and R)
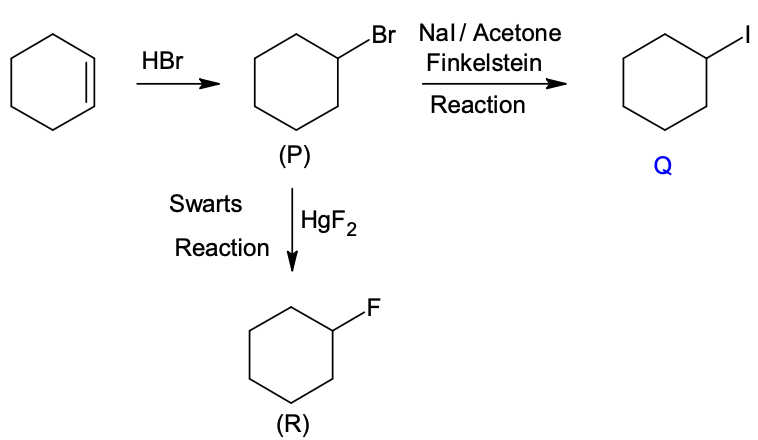 (In the options, X
(In the options, X
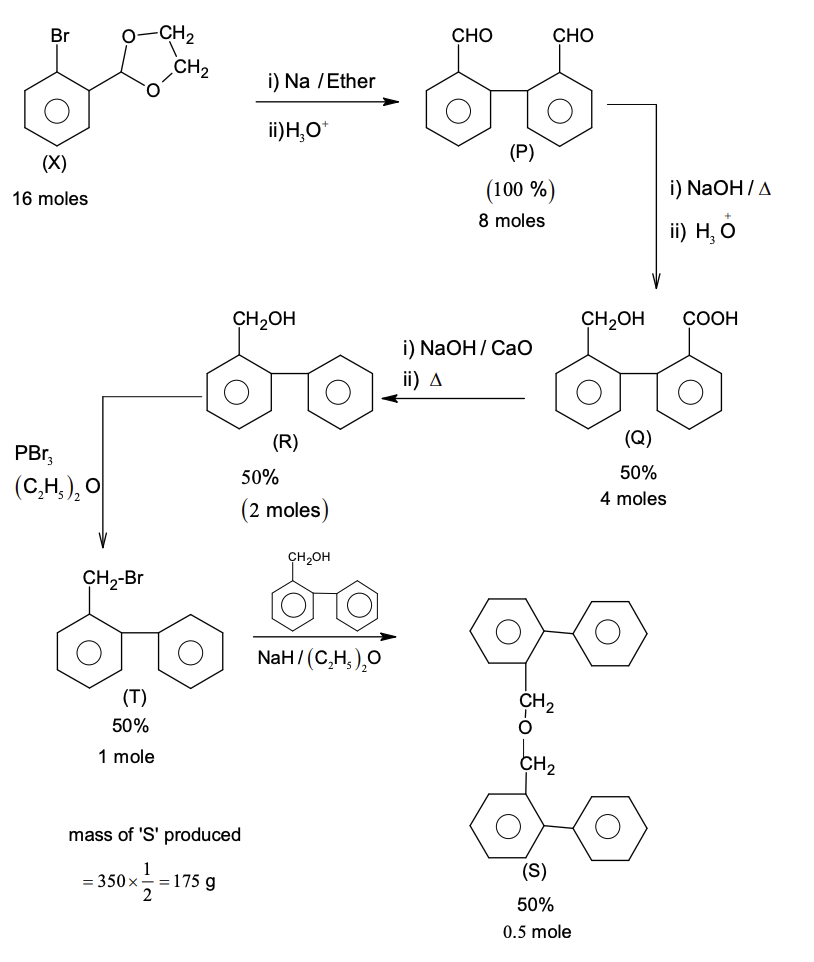
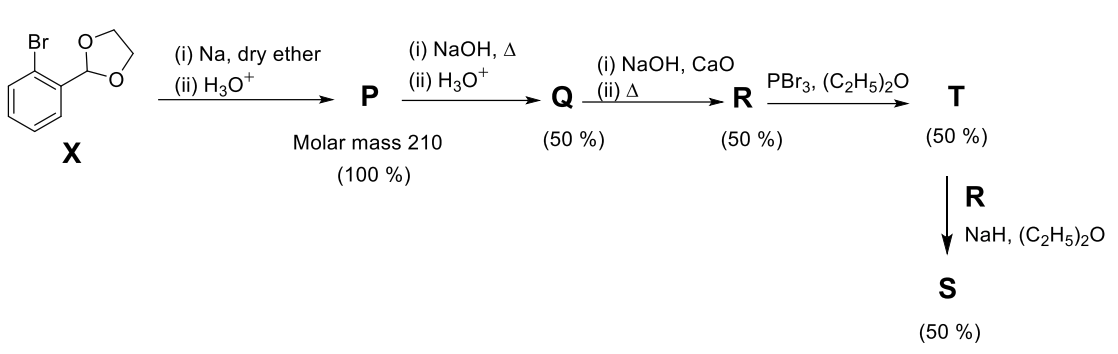 Use: Atomic mass (in amu): $\text{H} = 1, \text{C} = 12, \text{O} = 16, \text{Br} = 80$
Use: Atomic mass (in amu): $\text{H} = 1, \text{C} = 12, \text{O} = 16, \text{Br} = 80$