Then which one of the following statements is TRUE?
Solution
Given the condition $e^{x_0} + x_0 = 0$, we have $e^{x_0} = -x_0$.
We need to find $\alpha$ such that the limit exists and evaluate it. Let's test the option $\alpha = 3$.
The function is defined as:
$$g(x) = \frac{3xe^x + 3x - \alpha e^x - \alpha x}{3(e^x + 1)}$$Substitute $\alpha = 3$:
$$g(x) = \frac{3xe^x + 3x - 3e^x - 3x}{3(e^x + 1)} = \frac{3xe^x - 3e^x}{3(e^x + 1)} = \frac{3e^x(x - 1)}{3(e^x + 1)} = \frac{e^x(x - 1)}{e^x + 1}$$Now, substitute this simplified $g(x)$ into the limit expression:
$$L = \lim_{x \to x_0} \left| \frac{g(x) + e^{x_0}}{x - x_0} \right| = \lim_{x \to x_0} \left| \frac{\frac{e^x(x - 1)}{e^x + 1} + e^{x_0}}{x - x_0} \right|$$Combine terms in the numerator:
$$L = \lim_{x \to x_0} \left| \frac{e^x(x - 1) + e^{x_0}(e^x + 1)}{(e^x + 1)(x - x_0)} \right|$$Let the numerator function be $N(x) = e^x(x - 1) + e^{x_0}(e^x + 1)$.
Substitute $e^{x_0} = -x_0$ into $N(x)$:
$$N(x) = e^x(x - 1) - x_0(e^x + 1) = xe^x - e^x - x_0e^x - x_0$$Check if $N(x_0) = 0$ to apply L'Hopital's Rule:
$$N(x_0) = x_0e^{x_0} - e^{x_0} - x_0e^{x_0} - x_0 = -(e^{x_0} + x_0) = 0$$The denominator $D(x) = (e^x + 1)(x - x_0)$ also approaches 0 as $x \to x_0$. Thus, we have a $0/0$ form. Apply L'Hopital's Rule:
Differentiate the numerator with respect to $x$:
$$N'(x) = \frac{d}{dx}(xe^x - e^x - x_0e^x - x_0) = (e^x + xe^x) - e^x - x_0e^x = xe^x - x_0e^x = e^x(x - x_0)$$Differentiate the denominator:
$$D'(x) = \frac{d}{dx}((e^x + 1)(x - x_0)) = e^x(x - x_0) + (e^x + 1)(1)$$Now evaluate the limit ratio at $x = x_0$:
$$L = \left| \frac{N'(x_0)}{D'(x_0)} \right| = \left| \frac{e^{x_0}(x_0 - x_0)}{e^{x_0}(x_0 - x_0) + (e^{x_0} + 1)} \right| = \left| \frac{0}{0 + e^{x_0} + 1} \right| = 0$$Since the limit is 0 for $\alpha = 3$, statement (C) is TRUE.
Option Distractor Reasons
Incorrect assumption that \(\alpha=2\) simplifies the function appropriately, likely leading to a non-zero limit or undefined expression.
Similar to option A, testing \(\alpha=2\) leads to an incorrect conclusion.
Incorrect evaluation of the limit for \(\alpha=3\). This might happen if there is a calculation error in applying L'Hopital's rule or substitution.
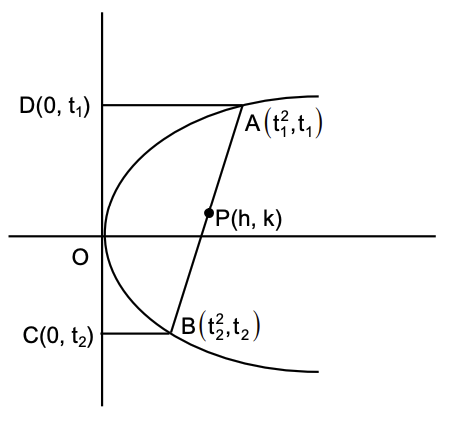 $$yk - \frac{1}{2}(x + h) = k^2 - h$$ $$2yk - x - h = 2k^2 - 2h \implies x = 2yk - (2k^2 - h)$$
$$yk - \frac{1}{2}(x + h) = k^2 - h$$ $$2yk - x - h = 2k^2 - 2h \implies x = 2yk - (2k^2 - h)$$
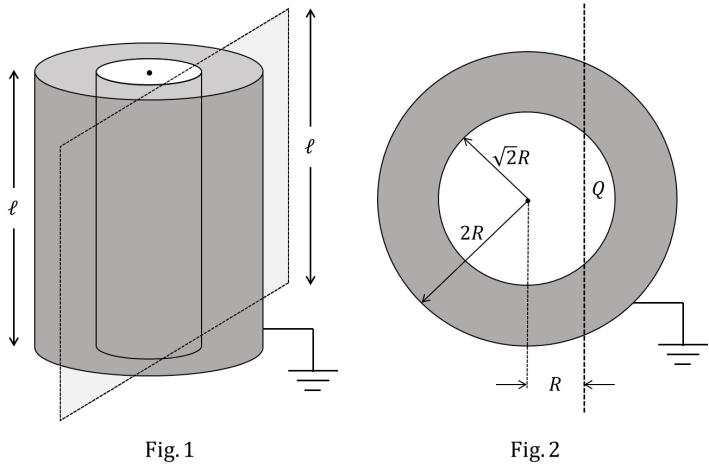
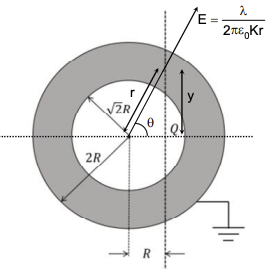 \[ E = \frac{\lambda}{2 \pi \epsilon_0 \kappa r} \] where \( \lambda = Q/l \) is the linear charge density, and \( \kappa = 5 \) is the dielectric constant. So, \( E = \frac{Q}{2 \pi \epsilon_0 (5) l r} = \frac{Q}{10 \pi \epsilon_0
l r} \).
\[ E = \frac{\lambda}{2 \pi \epsilon_0 \kappa r} \] where \( \lambda = Q/l \) is the linear charge density, and \( \kappa = 5 \) is the dielectric constant. So, \( E = \frac{Q}{2 \pi \epsilon_0 (5) l r} = \frac{Q}{10 \pi \epsilon_0
l r} \).